- 意味性錯語のプロットはやっていない。
- tSNE 上のプロットは 2 次元,かつ,分散 1 なので,項目間の相関係数が共分散に等しいのではないかな
\(^1\)クラーク病院, \(^2\)北海道大学, \(^3\)イムス板橋リハビリテーション病院, \(^4\)国際交流基金, \(^5\)静岡県立大学, \(^6\)目白大学, \(^7\)東京女子大学
要旨: 一般に,物品呼称課題あるいは絵画命名課題における心的処理プロセスは,語の意味に関する処理を含むと考えられている。 先行研究では意味の評価指標として,頻度・親密度・心像性の 3 つが用いられてきたものの,これらの指標はいずれも意味を直接表現してはいない。 本発表では,自然言語処理分野で用いられている単語埋め込みモデルを用いることにより,言語の持つ多様な意味表象を多次元ベクトルとして表現することを試みた。 これにより,意味性錯語や実験結果を定量的に記述・評価・視覚化することが可能となる。 例えば,「医者」という語の産出を意図した訓練場面において,または,心理実験場面において,「病院」や「学校」を手がかり語(あるいはプライム語)とした場合の効果量を,単語間の類似度として数値化可能である。 従来指標に比べて,単語埋め込みモデルによる単語間の類似度は,より意味を直接的に説明することを可能にすると考えられる。
キーワード: 意味性錯語, 単語海込みモデル, 潜在空間, tSNE,
1. はじめに
語の意味を定量化する試みは,長年試みられている。 とりわけ,刺激語と表出語との間の類似性を定量化できれば,診断,治療,回復計画などへの示唆が期待できる。 我々は,単語埋め込みモデルと潜在空間への確率的隣接埋め込みモデルを用いて,語の定量化を試み,意味性錯語の計量化を試みたので報告する。
ここでは,単語表象として,word2vec(Mikolov, Yih, and Zweig 2013; Mikolov et al. 2013) を,潜在空間モデルとして tSNE (Maaten and Hinton 2008) を用いることとした。 Word2vec や transformer(Vaswani et al. 2017) のごとき単語埋め込みモデルと, tSNE などの確率的隣接埋め込みモデルを用いた次元削減技法とは,共に機械学習,人工知能分野では人口に膾炙している。 しかし,我々の知る限り,これら両手法を用いて,意味性錯語の定量化を試みた例は少ないようである。 ここでに示す手法を用いることにより,従来手法に比べて,意味性錯語の評価に対して,目的語と表出語との間に,直接的な定量化が可能となる。
神経心理学において,単語の計量データとしては,頻度,親密度,心像性などが用いられる。 TLPA の 200 項目には,親密度の高低が区別されているが,親密度や心像性は,意味そのものの表現ではない(藤田 et al. 2000)。 それらは,評価データであり,課題遂行を記述するための独立変数というよりも,従属変数であると考えられる。 他の根拠から,これら評価値を独立変数として扱う研究も散見される。 しかし,従属変数を独立変数としてみなすことは,現象を直接説明するのではなく,間接的な説明になる。 このため,構成概念としての評価値を用いた,間接的な評価になる。 さらには,循環論法に陥る可能性もある。 そのため,直接的な独立変数を採択することが望まれる。
得られた単語表現を潜在空間へ射影することの意味は,脳内の領野間の結合については,確率的なサンプリングとして考えることが提案されている。 例えば,ドロップアウト(Hinton et al. 2012), 予測符号化(Friston, Kilner, and Harrison 2006), 変分自動符号化器(Kingma and Welling 2019), ヘルムホルツマシン(Dayan et al. 1995) などが挙げられる。 これらのモデルは,ボトムアップおよびトップダウンの大脳皮質処理経路の機能に関連するモデルとして提案されてきた。 本稿で提案する,単語表象と潜在意味空間との間には,上位層と下位層と間での前向き,逆向きの確率的依存関係が仮定される。 すなわち,種々の言語課題において,目標語と産出語との関係は互いに確率的認識モデル,生成モデルの関係と解釈される。
確率モデル例として下図に(Friston, Kilner, and Harrison 2006) の図 5 を示した。
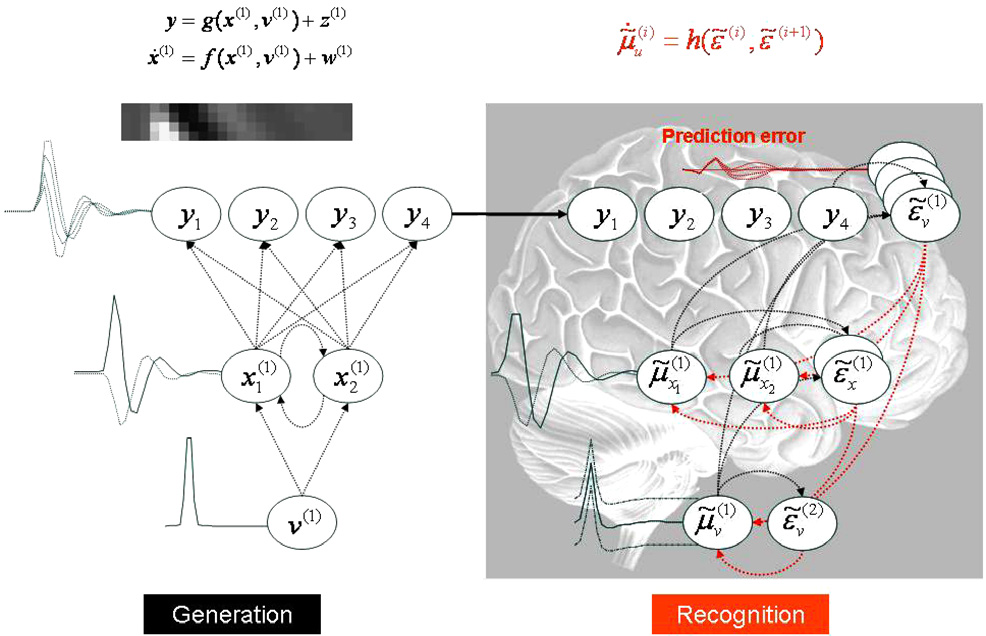
シミュレーションに用いた生成モデル (左) とそれに対応する認識モデル (右) を示す図。 左図:単一の原因 \(v(1)\), 2 つの動的状態 \(x_1,x_2\), 4 つの出力 \(y_1,\dots,y_4\) を用いた生成モデル。 線はそれぞれの変数の依存関係を示しており,上式で要約されている (この例では, どちらの式も単純な線形マッピング)。 これは事実上, 線形畳み込みモデルであり, 1 つの原因を 4 つの出力に写像し, それらが認識モデルの入力となる (実線の矢印)。 対応する認識モデルのアーキテクチャを右に示す。 予測誤差ユニット \(\hat{e}_u^{(i)}\) が含まれていることを除けば,同様のアーキテクチャである。 前向き推論 (赤線) と後向き推論 (黒線) を組み合わせることで, 自己組織化するリカレントダイナミクスが可能になる (認識式 \(\hat{\dot{u}}_u^{(i)}=h\left(\hat{\epsilon}^{(i)},\hat{\epsilon}^{(i)}\right)\) に従う)。 予測誤差を抑制し, できれば予測誤差をなくすことで, 推測される原因と実際の原因が一致する。 (Friston, Kilner, and Harrison 2006) Fig. 5 より
ここでは,2 節で word2vec と tSNE とを概説し,3 節で,数値実験結果と臨床例の解釈を示す。 4 節ではそれらのまとめて考察を加えている,5 節で結論を述べる。
2. 関連研究
単語埋め込みモデルは,単語をベクトルとして表現する手法である。 これには,潜在意味解析 LSA (Landauer and Dumais 1997),潜在ディレクリ配置 LDA (Blei, Ng, and Jordan 2003),など先駆的研究が挙げられる。 しかし,LSA や LDA では word2vec の示すような特徴,すなわち意味と文法知識とを同時に扱うことが,可能であるとしても困難である。 加えてニューラルネットワークによる実装を考えても,単語埋め込みモデルの方が有利であると考える。
これらのモデルと単語埋め込みモデルが異なるのは,単語の意味は,その前後の単語によって定まるとする点にある。 単語の意味を,前後の隣接語から定義する試みは,言語学の初期から提案されてきた(Harris 1954; Firth 1957)。 我々も,文中に未知単語を見つけた場合には,前後の文から未知単語を類推しようと試みることからも,このような意味の定義は納得できるものと考える。
得られた単語表現から,その類似度に基づいて 2 次元の附置を得る手法のうち tSNE を採択した。 tSNE を採択した理由は,その潜在空間との確率的解釈を持ちいて附置得る点にある。 一般に,データは決定論的に得られるわけではなく,むしろ確率的解釈が適当な事例が存在する。 量子論的宇宙観から神経心理学検査におけるデータの再現性まで,確率論的解釈は各所に偏在している。 また,ディープニューラルネットワークにおけるドロップアウト手法(Hinton et al. 2012) は,中間層表現に確率的解釈を導入する試みとも解釈できる。 このため,確率的解釈を行うことは,神経心理学データの解釈のみならず,昨今の機械学習手法の趨勢を鑑みても妥当な手法であると考えられる。
本稿では,両手法の取り上げた理由を概説し(2節),数値例を示す(3節)。 これにより,神経心理学への適用可能性を議論する(4節)。
2.1 単語埋め込みモデル word2vec
単語埋め込みモデル Word2vec には,2 種類ある。それらは CBOW と skip-gram と呼ばれる。 CBOW は,単語を逐次入力して,前後の単語から中央の単語を予測する。 一方 skip-gram は,反対に中央の単語から周辺のの単語を予測するモデルである(下図)。 word2vec の両モデルとも,3 層のフィードフォワードモデルである。 このとき,中間層ニューロン数と,単語前後の窓幅はハイパーパラメータである。 本稿では,中間層ニューロン数を 200 とし,単語窓幅は 20 とした。

左: CBOW モデル。右: skip-gram モデル。いずれのモデルでも同様の結果を得ることができる。 両モデルの中間層の活性値を,その単語の意味表現と考えるのが word2vec である。 より
Word2vec の特徴としては,単語ベクトルを用いて演算を行うことができることである。 「王」ー「男」+「女」=「女王」という類推が知られている(下図左)。 このような単語の意味に関するベクトルの加減算を用いた類推以外に,単語の単数形と複数形のような文法知識 (下図中央),あるいは,国名とその首都の関係 (下図右)が挙げられる。 下図右は,各国の国名と対応する首都名を取り出して,PCA による附置である。 横軸の右側に国名,左側に対応する首都名が附置されている。 一方,縦軸は上から下に向かって,ユーラシア大陸を東から西に大まかに並んでいるのが見て取れる。


word2vec の結果の附置の例。左: 単語の性を表す対応関係。中央: 単語と対応する複数形を表す。 word2vec は単語の意味関係だけでなく,複数形のような,文法的知識も表現可能である。 右: 各国名と対応する首都の関係の附置。
上述のごとく,word2vec などの単語埋め込みモデルは,単語の意味の持つ多様な側面を捉えているとみなしうる。 このような単語の特質は,親密度や心像性といった評価値では捉えることが難しい側面であると考えられる。 このような単語埋め込みモデルの持つ,単語の意味特性を用いることで,意味性錯語を定量化することが可能であろうと考えられる。
2.2 確率的隣接埋め込みモデル
意味性錯語を捉える場合に,単語の表現を低次元の地図に附置すると視覚化が容易になる。 機械学習分野では,高次元データを低次元附置をえる次元削減手法が種々提案されている。 伝統的には,主成分分析 (PCA) (Pearson 1901),コホネンの自己組織化マップ(コホネン 1997) などが枚挙に暇がない。 その中で,t 分布を用いた確率的隣接埋め込みモデル (tSNE) は人口に膾炙している (例えば https://colah.github.io/posts/2014-10-Visualizing-MNIST/)。
ここでは,tSNE の概略を説明し,TLPA による意味性錯語例がどのように解釈されるかを示すこととする。 高次元データを効率よく次元圧縮するためには,PCA などに加えて, 確率的解釈を導入することにより見通し良く視覚化できる。 確率的隣接埋め込みモデルとは,データ対の類似度,あるいは距離を,低次元の地図点に移す際に, 確率モデルを導入する。
tSNE は, データ点間の高次元ユークリッド距離を, 類似性を表す条件付き確率に変換する。 データ点 \(x_j\) とデータ点 \(x_i\) の類似性は, \(x_i\) を中心とするガウス分布の下で確率密度に比例して隣接点が選ばれた場合に,\(x_i\) が \(x_j\) を隣接点として選ぶ条件付き確率 \(p_{j\vert i}\) とする。 近傍にデータ点がある場合, \(p_{j\vert i}\) は類似度を高くし,遠く離れたデータ点間の場合,\(p_{j\vert i}\) はほぼ無限大にする (ガウスの分散 \(\sigma_i\) が妥当な値の場合)。数学的には, 条件付き確率 \(p_{j\vert i}\) は次のように与えられる:
\[
p_{j\vert i} = \frac{\exp\left(-\frac{1}{2}\frac{\left\|x_i-x_j\right\|^2}{\sigma_i^2}\right)}
{\sum_{k\ne j}\exp\left(-\frac{1}{2}\frac{\left\|x_i-x_k\right\|^2}{\sigma_i^2}\right)},
\]
ここで \(\sigma_i\) は,データ点 \(x_i\) を中心とするガウス分布の分散である。 ここでは, 一対の類似性のモデル化にのみ関心があるので,\(p_{i\vert i}\) の値をゼロに設定する。 高次元データ点 \(x_i\) と \(x_j\) の低次元対応点 \(y_i\) と\(y_j\) については, 類似した条件付き確率を計算することが可能であり, これを \(q_{j\vert i}\) とする。 条件付確率 \(q_{j\vert i}\) の計算に用いられるガウスの分散を \(\frac{1}{\sqrt{2}}\) とする。 したがって, 地図点 \(y_j\) と地図点 \(y_i\) の類似性を次のようにモデル化する:
\[
q_{j\vert i} = \frac{\exp\left(-\left\|y_i-y_j\right\|^2\right)}
{\sum_{k\ne j}\exp\left(-\left\|y_i-y_k\right\|^2\right)},
\] ここで, 我々は対ごとの類似性をモデル化することにのみ関心があるので,\(q_{i\vert i}=0\) とする。
地図点 \(y_i\) と \(y_j\) が高次元地図点 \(x_i\) と \(x_j\) の類似性を正しくモデル化していれば, 条件付確率 \(p_{j\vert i}\) と\(q_{j\vert i}\) は等しくなる。 この観察結果に触発され, SNE は \(p_{j\vert i}\) と \(q_{j\vert i}\) の間のミスマッチを最小化する低次元データ表現 を見つけることを目的とする。 \(q_{j\vert i}\) が \(p_{j\vert i}\) をモデル化する忠実さの自然な尺度は, Kullback-Leibler divergence(この場合加法定数までのクロスエントロピーに等しい) である。 SNE は, 勾配降下法を用いて, すべてのデータポイントにおける KLダイバージェンス の合計を最小化する。 コスト関数 C は以下のように与えられる:
\[
C = \sum_i \text{KL}\left(P_i\vert\vert Q_i\right)=\sum_i\sum_j p_{j\vert i}\log\frac{p_{j\vert i}}{q_{j\vert i}}
\]
ここで,\(P_i\) はデータ点 \(x_i\) に対する他のすべてのデータ点の条件付き確率分布を表し,\(Q_i\) は地図点 \(y_i\) に対する他のすべての地図点の条件付き確率分布を表す。 KL ダイバージェンスは対称ではないため, 低次元地図の対毎の距離の異なるタイプの誤差は均等に重み付けされない。 特に, 近くのデータ点を表現するために大きく離れた地図点を使用する (つまり, 大きな \(p_{j\vert i}\) をモデル化するために小さな \(q_{j\vert i}\) を使用する) ことには大きなコストがかかるが, 大きく離れたデータ点を表現するために近くの地図点を使用することには小さなコストしかかからない。 この小さなコストは, 関連する \(Q\) 分布の確率量の一部を無駄にしていることに由来する。 言い換えれば, SNE コスト関数は, 地図内のデータの局所的な構造を保持することに重点を置いている (高次元空間におけるガウスの分散の妥当な値 \(\sigma_i\) の場合)。
高次元空間では, ガウス分布を用いて距離を確率に変換する。 低次元地図では, ガウス分布よりもはるかに重い尾を持つ確率分布を使って, 距離を確率に変換することができる。 これにより, 高次元空間での適度な距離は, 地図上でははるかに大きな距離によって忠実にモデル化され, その結果,適度に似ていないデータ点を表す地図上の点間の不要な引力を排除することができる。
t-SNE では, 低次元地図の重尾分布として, 自由度 1 のスチューデントの t 分布 (コーシー分布に等しい) を採用している。 この分布を用いて, 結合確率 \(q_{ij}\) を以下のように定義する:
\[
q_{ij} = \frac{\left(1+\left\|y_i-y_j\right\|^2\right)^{-1}}{\sum_{k\ne l}\left(1+\left\|y_k-y_l\right\|^2\right)^{-1}}.
\]
低次元の地図において, 大きな対の距離 \(\left|y_i-y_j\right|^2\) に対して, \(\left(1+|y_i-y_j|^2\right)^{-1}\) が逆二乗法に近づくという, 特に優れた特性を持っているからである。 これにより, マップの結合確率の表現は, 遠く離れた地図点の地図の尺度の変化に (ほとんど) 影響されない。 また, 遠く離れた点の大規模なクラスターは, 個々の点と同じように相互作用するため, 最適化は微細なスケールを除いて同じように作用することになる。 スチューデントの t 分布を選択した理論的な理由は, スチューデントの t 分布がガウス分布の無限混合であるように, ガウス分布と密接に関連しているからである。
t 分布確率的隣接埋め込みモデル (tSNE) を用いて,意味空間を視覚化することにより,意味空間を把握しやすくなる。 具体的には,高次元の意味空間を P とし,P より低次元の意味空間を Q とする。 P から Q への写像は,確率的なされると考える。 このとき,P と Q と両分布の距離を最小にするような写像を考える。両分布の相違をカルバック・ライブラーのダイバージェンスで定義すれば:
\[
C = \text{KL}\left(P\vert\vert Q\right)=\sum_i\sum_j p_{ji}\log\frac{p_{ji}}{q_{ji}}
\]



手書き文字認識データセット MNIST 6000 字を可視化したもの。
tSNE を理解を促すために,優れたサイトが公開されている。 今回,その邦訳を用意した。関心があれば参照されたい 効率よく t-SNE を使う方法
3. 数値実験
単語埋め込みモデルとして,日本語ウィキペディア (https://dumps.wikimedia.org/jawiki/latest/) を mecab + NEologd (https://github.com/neologd/mecab-ipadic-neologd}) によってて分かち書きし, word2vec (https://code.google.com/archive/p/word2vec/} により単語埋め込みベクトル化した。 Skip-gram を使用し,ベクトル化した際のパラメータは,埋め込みベクトル次元:200,ウィンドウ幅:20,負例サンプリング:20 とした。 出現頻度 5 回以上の単語のみを考慮することとし,総語彙数 180,543 語を得た。
3.1 TLPA
TLPA 200 語の結果を下図に示す。 下図左が tSNE,右図は PCA のプロットである。


左図: TLPA 200 語の tSNE プロット,色の違いはカテゴリの違いを表す。
右図: 左と同じデータをもちいた PCA プロット。 カテゴリーは,乗り物, 色, 植物, 加工食品, 建造物, 道具, 野菜果物,身体部位, 屋内部位, 動物 の 10 種類
TLPA はカテゴリー毎の記述があるので,カテゴリー毎に色分けして描いた。 左右両図とも,大まかにカテゴリ毎に群化しているように見受けられる。 しかし,左図 tSNE の方が,群化が著しいように見受けられる。
各カテゴリーごとにまとめて,分散を tSNE と PCA で比較すると群化の程度が数値化できるけど,まだやっていない。
上記結果を確認するためのコードを用意した。 tSNE による TLPA 検査語彙 200 項目のプロット ソースコード 
3.2 SALA
SALA PR20 呼称 I 96 語と PR24 呼称 II 90 語の計 196 語を用いて同様のプロットを作成した図を以下に示す。


SALA PR20 呼称 I 96 語と PR24 呼称 II 90 語の tSNE プロット。色の違いは, PR20, PR24 の違いを表している。
3.3 ResNet による視覚情報のプロット
意味的関係が適切に群化される一方で,視覚入力情報は,どのように潜在空間へ写像されるのだろうか。 このことを確認するため,上述の TLPA, SALA と描画と同じ手法を用いて ResNet(He et al. 2015) の最終直下層の情報を描画した(下図)。


図 視覚入力の tSNE プロット。 左: SALA, 右: TLPA
4. 考察
5. まとめ
今後の検討に期待する。 うんだらかんたら,以下略。
文献
Blei, David M., Andrew Y. Ng, and Michael I. Jordan. 2003. “Latent Dirichlet Allocation.” Journal of Machine Learning Research 3: 993–1022.
Dayan, Peter, Geoffrey E. Hinton, Radford M. Neal, and Richard S. Zemel. 1995. “The Helmholtz Machine.” Neural Computation 7: 889–904.
Firth, John R. 1957. A Synopsis of Linguistic Theory 1930-55. Vols. 1952-59. Oxford: The Philological Society.
Friston, Karl, James Kilner, and Lee Harrison. 2006. “A Free Energy Principle for the Brain.” Journal of Physiology 100: 70–87.
He, Kaiming, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. 2015. “Deep Residual Learning for Image Recognition.” ArXiv:1512.033835.
Hinton, Geoffrey E., Nitish Srivastava, Alex Krizhevsky, Ilya Sutskever, and Ruslan R. Salakhutdinov. 2012. “Improving Neural Networks by Preventing Co-Adaptation of Feature Detectors.” The Computing Research Repository (CoRR) abs/1207.0580. http://arxiv.org/abs/1207.0580.
Kingma, Diederik P., and Max Welling. 2019. “An Introduction to Variational Autoencoders.” Foundations and Trends in Machine Learning: 12 (4): 307–92. https://doi.org/doi:10.1561/2200000056.
Landauer, Thomas K., and Susan T. Dumais. 1997. “A Solution to Plato’s Problem: The Latent Semantic Analysis Theory of Acquistion, Induction, and Representation of Knowledge.” Psychological Review 104: 211–40.
Maaten, Laurens van der, and Geoffrey Hinton. 2008. “Visualizing Data Using T-Sne.” Journal of Machine Learning Research 9: 2579–2605.
Mikolov, Tomas, Ilya Sutskever, Kai Chen, Greg S. Corrado, and Jeff Dean. 2013. “Distributed Representations of Words and Phrases and Their Compositionality.” In Advances in Neural Information Processing Systems 26, edited by C. J. C. Burges, L. Bottou, M. Welling, Zoubin Ghahramani, and K. Q. Weinberger, 3111–9. Curran Associates, Inc. http://papers.nips.cc/paper/5021-distributed-representations-of-words-and-phrases-and-their-compositionality.pdf.
Mikolov, Tomas, Wen-tau Yih, and Geoffrey Zweig. 2013. “Linguistic Regularities in Continuous Space Word Representations.” In Proceedings of the 2013 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies NAACL. Atlanta, WA, USA.
コホネンT. 1997. 自己組織化マップ. 2nd ed. 東京: シュプリンガー・フェアラーク.
藤田郁代, 物井寿子, 奥平奈保子, 植田恵, 小野久里子, 下垣由美子, 藤原由子, 古谷二三代, and 笹沼澄子. 2000. “「失語症語彙検査」の開発.” 音声言語医学 42: 179–2002.
