DaSiC 7 (2023) Linguistics and Data Science in Collaboration 発表資料
Shin Aasakawa, all rights reserved.
https://opensource.org/license/mit/
機械学習モデルの説明
--- N. Wiener, The Human Use of Human Beings(人間機械論, みすず書房, p.73) ---
Table of contents: part 2 第二部目次 (15:15-16:15)
- Dell+ モデルによるいい誤りのシミュレーション Dell+’s model for speech errors
- ソフトマックス関数の温度パラメータ thermal parameter in softmax function
- 患者ごとの微調整
- A encoder-decoder model for word repetition tasks
Table of contents: part 3 第三部目次 (16:25-17:40)
- A model of 百人一首 implemented on Transformer
- Horizontal and vertical errors in speech errors
WEAVER++, Dell モデルの再現シミュレーション colab files
- 他言語プライミング課題での事象関連電位 (ERP) のシミュレーション Roelofs, Cortex (2016)
- 概念バイアス
Conceptual Bias(Reolofs, 2016) 絵画命名,単語音読,ブロック化,マルチモーダル統合 - WEVER++ デモ 2020-1205 更新 Reolofs(2019) Anomia cueing
転移学習と微調整
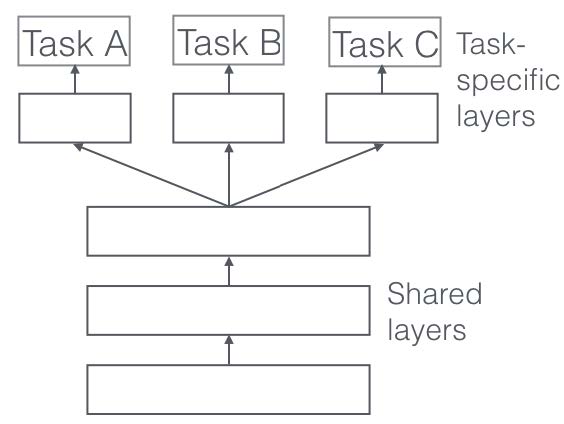
転移学習の応用例 (1) TLPA,SALA 失語症,絵画命名課題
絵画命名課題を一般画像認識モデルの転移学習として実現した。



転移学習の応用例 (2) BIT 行動注意検査線分二等分課題のシミュレーション (浅川,武藤 投稿中)
一般画像認識モデルにおける,場所情報 (were 経路) とその内容 (what 経路) を転移学習により実現
従来モデル
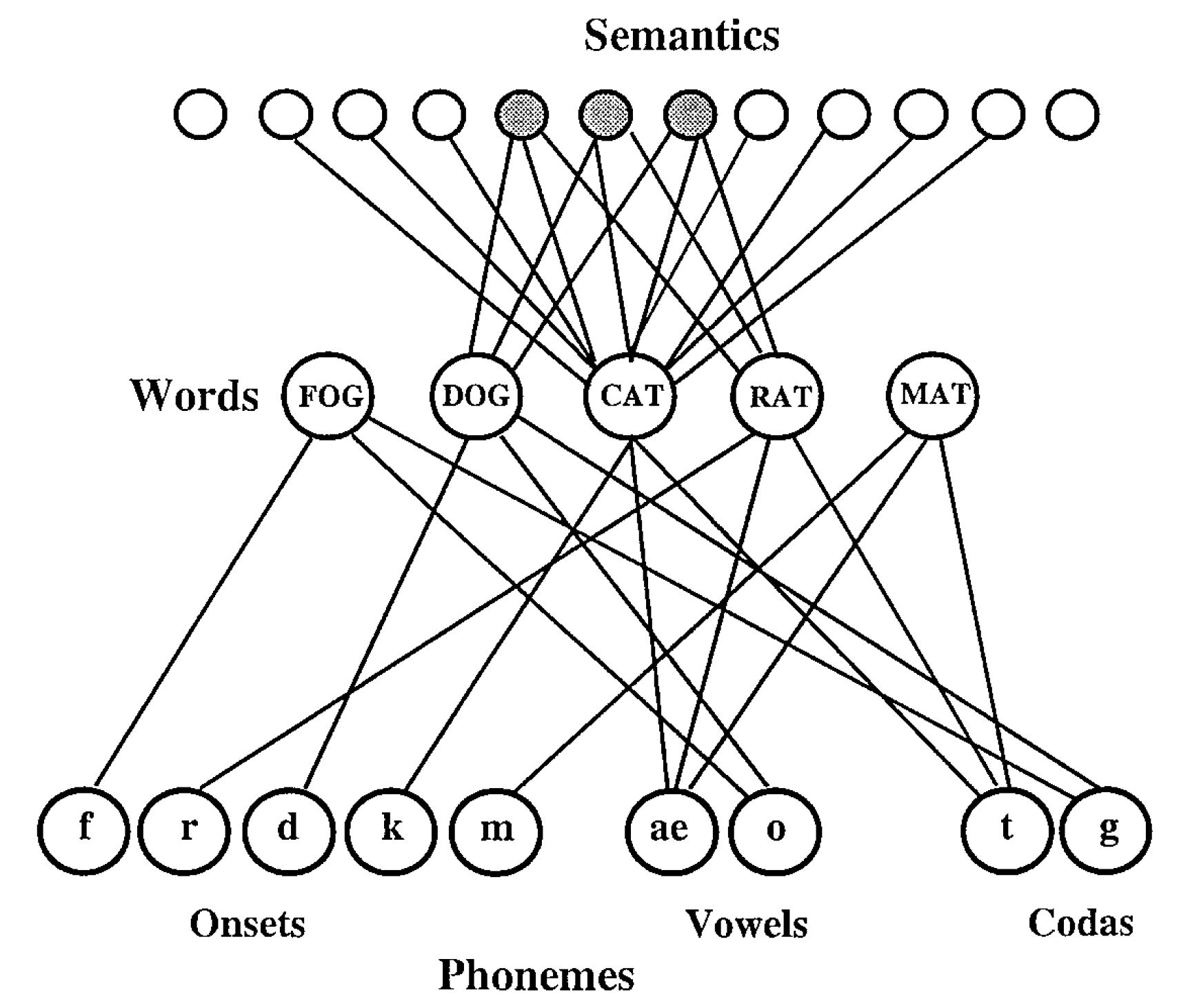
Dell モデルは,2 段階相互活性モデルであり,意味層,語彙層,音素層の 3 層からなるニューラルネットワークモデルである。 従来モデル (以下 Dell モデルと表記する) を図 1 (Foygel&Dell, 2000) に示した。 以下では,意味層を S 層,語彙層を L 層,音素層を P 層と表記する。 Dell モデルにおいては,ニューラルネットワークの特徴の一つである学習に基づくパラメータの調整は行われない。 このため Dell モデルを構成する各処理ユニット間の結合係数は一定である。 各層のユニット数は,S 層 10,L 層 5,P 層 9 個である。 Dell モデルの動作を略述すると以下のようになる: シミュレーションは離散時間で行われ,時刻 $t=[1,\ldots,16]$ の 16 時刻である。 時刻 $t_1$ で S 層には 3 つのユニットが活性化され,他の 7 つのユニットは不活性である。 S, L, P 層の $i$ 番目のユニットの活性値を,それぞれ $x_{i}$ $i\in$ $\left\{s,l,p\right\}$ とする。 任意の時刻 $t$ における各ユニットの活性値を表現する場合には,$x_{(i,t)}$ とする。 開始時刻 $t_1$ では S 層の 3 ユニットが必ず,活性化した状態,すなわち 1 にセットされ,残りの 7 つのユニットは 0 とされる。 活性化状態とされる 3 つのユニットは常に固定されて,シュミュレーションを通じて変化しない。 先述のように,離散化時刻が用いられるので,各ユニットは 16 回の更新を受けることとなる。 S 層と L 層,および L 層 と P 層とは相互に接続されているため,時刻 $t>1$ においては,結合している層間の影響を受け取る。 また,$t=8$ 時刻に,原著論文では jolt と命名された,最大値を強調する活性値の増強が行われる。 また,各時刻では,活性値の大きさに依存した乱数も付加される。 このため最終時刻 $t=16$ での L 層の活性値は,その都度変動することとなる。
Dell モデルでは,モデルを記述するための 4 つのパラメータ,s, p, w, d が用意されている。 s は S 層と L 層との結合係数に関わる係数,p は L 層と P 層とに関わる結合係数,w は結合係数全体に関わる結合係数であり,d 全ユニットの減衰率 (decay rate) である。 Dell モデルでは,s, p を調整可能なパラメータとする sp モデルと w, d を調整可能なパラメータとする wd モデルとが存在する。 sp モデルでは局在する結合係数の変動を記述する意味で,限局的パラメータであるということができる。 一方,wd モデルは,全処理ユニットに共通であるため,大域的パラメータとみなしうる。 すなわち sp モデルでは w と d は固定され,s と p との差異にのみ関心がある。 一方,wd モデルでは,限局したパラメータ変動を認めず ($w=s=p$),大域的パラメータの変動によって課題成績を説明しようとする。
Dell モデルの改善提案 (浅川+2019)
ソフトマックス関数における温度パラメータ
従来モデルの問題点
本稿では,上記 Dell モデルの記述をパラメータ推定問題として捉え,機械学習の手法を援用することでパラメータの推定を行うことを提案する。 しかし,以下の問題点が指摘できる。
- 入力刺激が,常に1 種類と極めて限られている。 入力は,常にネコ (CAT) を表す意味ベクトルのみである。 この入力に対する出力が,cat なら正解,dog なら意味エラー (semantic erros), mat なら形式エラー (formal errors), rat なら混合エラー (mixed errors), log なら無関連エラー (unrelated errors), さらに lat なら非単語 (non-word errors) あるいは新造語エラーとみなされる。 このように,従来モデルにより産み出されるエラーパターンは失語症者の呼称エラーに対応づけて検討されているものの,実際の検査や実験においては複数の異なる入力刺激が用いられることを鑑みれば,モデルにおける入力刺激の少なさは妥当性を欠くと言える。 また,入力刺激に対して,各概念は 10 個のニューロンを活性化し,かつ,概念同士の間で共有されるニューロンの存在が仮定されている(たとえばターゲット語 CAT と意味関連語の DOG の間では 3 個のニューロンの活性を共有している)ものの,これらのニューロン数と内容の設定根拠について詳述されていない点も,関連する問題として挙げることができるだろう。
- シミュレーションにおける刺激回数が少ない。 Foygel & Dell (2000) ではネコの画像を 175 回提示して,どの種のエラーが報告されたかを計数している。 175 という数字はフィラデルフィア絵画命名課題(Roach, Schwartz, Martin, Grewal,&Brecher, 1996) の試行数である 175 回と一致させるためである。 シミュレーションでは、ネコの呼称を 175 回繰り返して得られた 6 種類の反応カテゴリ(正答と 5 種類のエラー) の比率を最も良く表出するパラメータの値を探索するため,パラメータ値を定めて,175 回演算を繰り返し,得られた値からパラメータを探索している。 しかしながら,現代の技術から考えるとコンピュータは疲れを知らないので,精度を向上させるためには多数回繰り返すことを検討すべきだと言える。
- Jolt の大きさとタイミングに関する根拠が明白でない。 Jolt とは,特定のタイミングでモデルに与えられるブーストのことを指し,2 段階相互活性化モデルにおいては意味処理と語彙処理に対して与えられるよう設定されている。 すなわち,時刻 t が 1 のときには意味ブースト 10,t=8 のときには語彙ブースト 100 が付与され,モデルの処理が促進されると考えられている。 しかしながら,これらの値やタイミングの設定は恣意的であり,明確な根拠は示されていない。
- Dell モデルの出⼒は,被検査者の反応そのものをシミュレートするのでなく,反応を分類した結果を予測する。 このため従来モデルは,被検査者の課題遂⾏能⼒のみをシミュレートするものではなく,検査者の判断をも内包してしまっていると解釈できる。 そこで,今回提案する呼称モデルの改定案では、近年の機械学習分野における手法をモデル構築に取り入れることで,これらの問題点を解決することを試みた。
Dell モデルの改定 温度パラメータの変化
図 3 は,ソフトマックス関数において,温度パラメータを変化させた場合の各反応カテゴリーの確率密度の変化を示している。
温度パラメータ $\beta$ が 0 に近い(すなわち,健常者の反応をシミュレートしている)ときにはモデルは正解を算出しやすくなる。 一方,温度パラメータ $\beta$ が大きくなる場合,すなわち,患者の反応をシミュレートする場合には,各エラー率の値が上昇する。 $\beta$ は統計力学からの類推から温度パラメータと呼ぶことにする。 ソフトマックス関数は,ボルツマン分布と同一であって $x_i$ のエネルギー順位を与える式である。 このとき $\lim_{\beta\approx0}$ の極限では系は統計力学におけるボルツマン分決定論的に振る舞い $\lim\beta\mapsto\infty$ ではあらゆるエネルギー準位をとることとなる。 温度パラメータの導入意図は,このように系が確率的変動を許容する程度を表すものと解釈できるようにすることで,健常者と患者の呼称成績を連続的に捉えることを可能にするためであった。 すなわち,絵画命名課題において,健常者は温度パラメータが小さい,従って温度が低く安定した反応を生じることに対応する。 一方,反応が検査の都度変動するような,ある種の患者の錯語反応は,温度パラメータが大きい,従って温度が高いとみなしうる。 ソフトマックス関数については,ニューラルネットワークでの画像識別やカテゴリー判定などの分類課題に用いられている意味で汎用性が高い。
ソフトマックス関数を呼称課題の反応生成に使用した利点
また,相互活性化モデルの確率論的改訂である多項相互活性化モデル MIA (Multinomial Interactive Activation)モデル (McClelland, 2013; McClelland, Mirman, Bolger, & Khaitan, 2014) でも類似の概念が用いられている。 すなわち,本稿で提案するモデルは,オリジナルの IA モデルを拡張した MIA モデルの概念を援用して,絵画命名課題の妥当な解釈を行っているものとみなしうる。 ただし MIA モデルでは,温度概念を推定すべきパラメータとして扱っておらず,温度パラメータ $\beta$ を反応の安定性,あるいは多様性をとみなす考え方は,本提案手法に独自のものである。 また,ソフトマックス関数に温度パラメータを導入するアイデアは,ボルツマンマシン (Ackley, Hinton, & Sejnowski, 1985; Hinton & Sejnowski,1986) からの伝統である。 加えて,近年精度向上が著しい深層学習分野での自己半教師あり学習 (Self semi-suupervised learning でも採用されている概念でもある。 深層学習においては,ソフトマックス関数に温度パラメータ $\beta$ を導入することで,系の確率的振る舞いの変動を制御する意味合いがある (Chen, Konblith, Nouzi & Hinton, 2020; Jaiswal, Babuadeh, Makedon, 2020; Oord, Li, & Vinyals,2018)。 本手法では,確率的な振る舞いの度合いが,患者と健常統制群の課題成績を記述するパラメータであると考えことになる。 従って,ある種の患者の示す個々の反応は,都度都度変動し,決定論的な応答を得ることが少ない症例を模倣していることになると見なしうる。 一方,健常統制群の課題成績は,任意の刺激図版に対して安定的な応答が得られやすいと考えられる。 このことは,健常統制群の系では,温度パラメータ $\beta$ が低く,すなわち,系の応答が安定しているとみなすことなる。
患者ごとのシミュレーション結果 データは Foygell&Dell2000 論文中のデータを用いた
学習
教師信号 $\mathbf{t}=\left[0.97, 0.01, 0.00, 0.01, 0.00, 0.00\right]$ とする。 このとき最小化すべき目的関数(損失関数,誤差関数) $l$ を次のように定義する:
\[\tag{A.1} l\left(p,x;\theta\right)\equiv\sum_i\left( t_i\log(p_i) + (1-t_i)\log(1-p_i)\right)\] \[\tag{A.2} \frac{\partial l}{\partial p}=\sum_i\left( \frac{t_i}{p_i}-\frac{1-t_i}{1-p_i} \right) = \sum_i\frac{t_i(1-p_i)-p_i(1-t_i)}{p_i(1-p_i)} = \sum_i\frac{t_i-p_i}{p_i(1-p_i)}\]この $l$ を最小化する学習をニューラルネットワークの学習則に従い以下のような勾配降下法を用いて訓練する: \(\tag{A.3} \Delta\theta = \eta\frac{\partial l}{\partial\theta} = \eta\frac{\partial l}{\partial p}\frac{\partial p}{\partial x_t}\frac{\partial x_t}{\partial\theta}\)
合成関数の微分則に従って \(\tag{A.4} \frac{\partial l}{\partial\theta}\) である。
更に $p_{i}$ を $x_{j,t}$ で微分,すなわちソフトマックスの微分:
\[\tag{A.5} \begin{aligned} \frac{\partial p_{i}}{\partial\beta x_{i}} =\frac{e^{\beta x_{i}}\left(\sum e^{\beta x_{j}}\right)-e^{\beta x_i}e^{\beta x_{i}}}{\left(\sum e^{\beta x_{j}}\right)^{2}} &=\left(\frac{e^{\beta x_{i}}}{\sum e^{\beta x_{j}}}\right) \left(\frac{\sum e^{\beta x_{j}}}{-e^{\beta x_{j}}}{\sum e^{\beta x_{j}}}\right)\\ &=p_i \left(\frac{\sum e^{\beta x_{j}}}{\sum e^{\beta x_{i}}}-\frac{e^{\beta x_{i}}}{\sum e^{\beta x_{j}}}\right)\\ &=p_i (1-p_{j})\frac{\partial p_{i}}{\partial x_{j}} \\ &= p_i(\delta_{ij}- p_{j})\\ \frac{\partial p_{i}}{\partial x_{j}} &= p_{i}\left(\delta_{ij}- p_{j}\right) \end{aligned}\]$\theta$ を $\beta$ とそれ以外 ($w,d,s,p$) とに分けて考える。 更に,各個のパラメータについて微分することを考える。 Dell らのモデルでは次式のような漸化式が用いられた: \(x_{t+1} = (1-d)x_{t} + \sum w x_{t} + z,\tag{A.7}\)
ここで $z\sim\mathcal{N}\left(0,a_1^2 + a_2^2x_{t}\right)$ である。
\[\Delta \theta=\eta\frac{\partial l}{\partial\theta}\tag{A.8}\]ここで $l$ は損失関数 (誤差関数,目的関数) であり,(\eta) は学習係数 (learning ratio) である。
\[\begin{aligned} \frac{\partial l}{\partial\theta} &=\frac{\partial l}{\partial p}\frac{\partial p}{\partial x_t}\frac{\partial x_t}{\partial\theta}\\ &=\sum_i\frac{t_i-p_i}{p_i(1-p_i)}\sum_j p_i\left(\delta_{ij}-p_j\right)\frac{\partial x_{j,t}}{\partial\theta}\\ \end{aligned}\tag{A.9}\]今一度,損失関数を (l), 最終層出力の出力を確率密度関数を $y$, 各ニューロンの出力値を $x$ とする。 推定すべき Dell モデルのパラメータ $\theta={w,d,s,p}$ とする。
それぞれ以下の通りである:
- $w$: 重みパラメータ
- $d$: 崩壊パラメータ
- $s$: 視覚入力層と語彙層との間の結合パラメータ
- p$: 語彙層と音韻層との結合パラメータ
$x_{i,\tau}^{(\text{Layer})}$ を $\text{Layer}=\left[s:\text{視覚的意味層}, l:\text{語彙層}, p:\text{音韻層}\right]$ を時刻 $\tau$ での層 (Layer) における $i$ 番目のニューロンであるとすれば,次式を得る:
\[\begin{array}{ll} x_{i,t+1}^{(s)} &= (1-d)x_{i,t}^{(s)} + sw \sum_j u_{ij}^{(l)}x_{j},\\ x_{i,t+1}^{(l)} &= (1-d)x_{i,t}^{(l)} + sw \sum_{j\in(s)} u_{ij}^{(s)}x_{j}^{(s)} + pw\sum_{j\in(p)}u_{ij}^{(p)} x_j^{(p)},\\ x_{i,t+1}^{(p)} &= (1-d)x_{i,t}^{(p)} + pw \sum_{j\in(l)} u_{ij}^{(l)}x_{j}^{(l)},\\ \end{array}\tag{A.10}\]\(\mathbf{\Theta}= \left( \begin{array}{ccc} 1-d & wp & 0\\ wp & 1-d & ws\\ 0 & ws & 1-d\\ \end{array} \right)\tag{A.11}\) とすれば,
\[\mathbf{x}_t=\mathbf{\Theta x}_{t-1}+ z\left(\mathbf{x}_{t-1};a_1^,a_2^2\right)\tag{A.12}\]コード
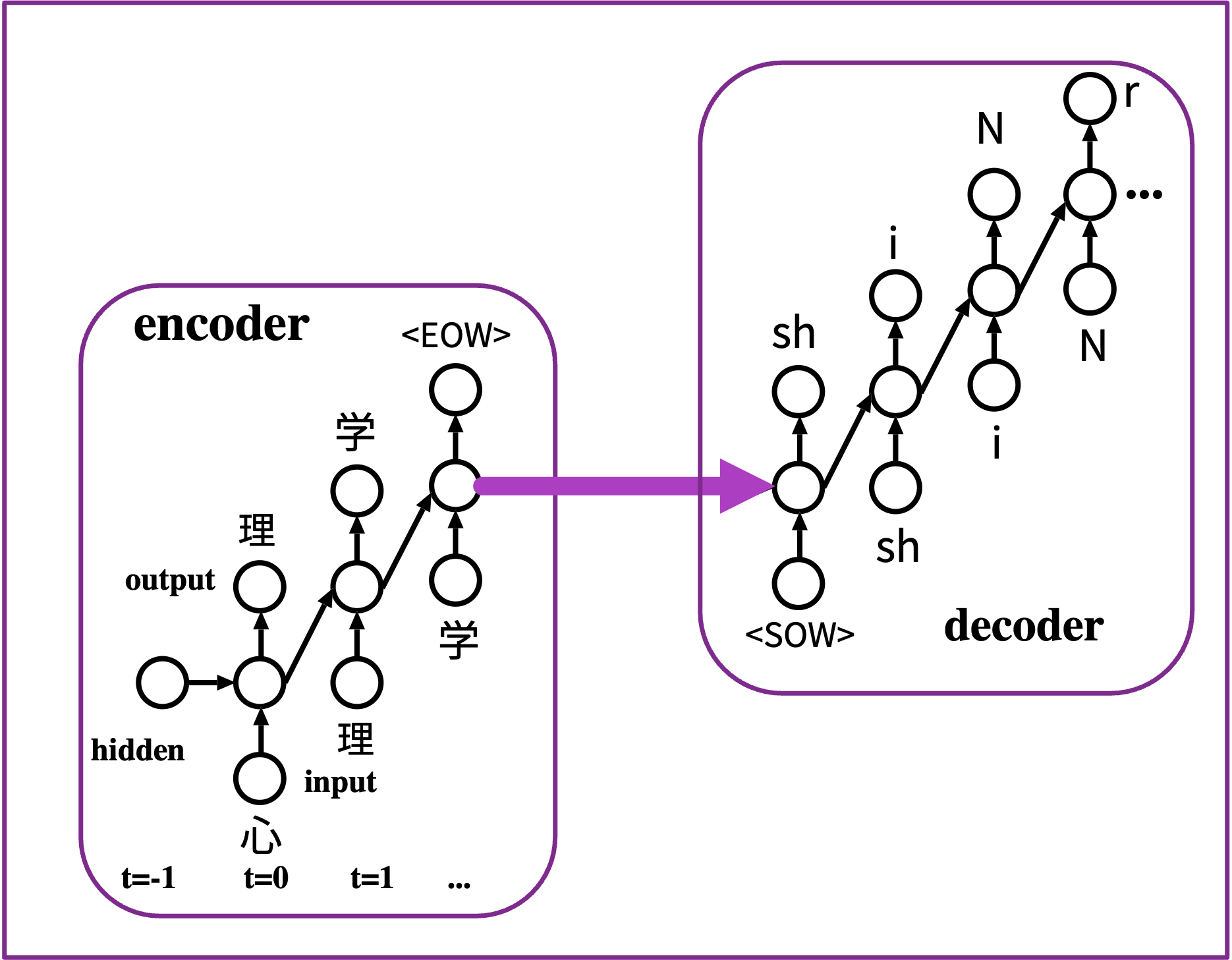
エンコーダ・デコーダモデルを用いた,健常者と失語症患者の言い誤りのシミュレーション (大門+2023)
翻訳モデルにおける注意
- 符号化器の最後の隠れ状態から単一の文脈ベクトルを構築するのではなく,文脈ベクトルとソース入力全体との間にショートカットを作成する。
- これらのショートカット接続の重みは,各出力要素ごとにカスタマイズ可能
- 文脈ベクトルが全入力系列にアクセスできる間は,忘れる心配はない。
- ソースとターゲットの間のアライメントは,文脈ベクトルによって学習され,制御される。
- 基本的に文脈ベクトルは 3 つの情報を用いる。
- 符号化器側の中間層状態 (ソース)
- 復号化器側の中間層状態 (ターゲット)
- ソースとターゲットのアラインメント(配置情報) すなわちどの位置の情報に着目すべきかを決定する
2.2 注意の種類
-
文脈ベースの注意 Content-base attention (Graves2014): $\text{score}(\mathbf{s}_t, \mathbf{h}_i) = \cos\left(\mathbf{s}_t, \mathbf{h}_i\right)$
- 加算的注意 Additive attention (Bahdanau2015):
$\text{score}(\mathbf{s}_t, \mathbf{h}_i) =$ $\mathbf{v}_a^\top \tanh(\mathbf{W}_a\left[\mathbf{s}_t; \mathbf{h}_i\right])$
Loung2015 論文では,”concat”, Vaswani2017 論文では “additive atttention” として言及されている注意のこと - 位置ベースの注意 Location-Base attention (Luong2015):
$\alpha_{t,i} = \text{softmax}(\mathbf{W}_a\mathbf{s}_t)$
これにより,ソフトマックス配置(アライメント)がターゲット位置のみに依存するように単純化される。 - 一般化注意 General attention (Luong2015):
$\text{score}(\mathbf{s}_t,\mathbf{h}_i) = \mathbf{s}_t^\top\mathbf{W}_a\mathbf{h}_i$
$\mathbf{W}_a$ は,注意層の訓練可能な重み行列 - 内積型注意 Dot-Product attention attention (Luong2015): $\text{score}(\mathbf{s}_t,\mathbf{h}_i) = \mathbf{s}_t^\top\mathbf{h}_i$
- 規格化内積型注意 Scaled Dot-Product attention (Vaswani2017):
$\text{score}(\mathbf{s}_t, \mathbf{h}_i) = \frac{\mathbf{s}_t^\top\mathbf{h}_i}{\sqrt{n}}$
注:尺度因子を除いて内積型注意に酷似する;ここで、n はソース中間層状態の次元。 BERT および GPT で用いられている。
$[\cdot;\cdot]$ は 2 つのベクトルの連接を表す。
2.3 注意の定義
長さ $n$ のソース系列 $\mathbf{x}$ と,長さ $m$ のターゲット系列 $\mathbf{y}$ を考える。 太字はベクトルであることを示す。
\[\begin{aligned} \mathbf{x} &= \left[x_1, x_2, \dots, x_n\right] \\ \mathbf{y} &= \left[y_1, y_2, \dots, y_m\right] \\ \end{aligned}\]復号化器ネットワークは,位置 $t$ の出力語に対して隠れ状態 $\mathbf{s}t=f( \mathbf{s}{t-1}, y_{t-1}, \math bf{c}_t)$, $t\in[1,m]$ であり,文脈ベクトル $\mathbf{c}_t$ は入力系列の隠れ状態の和で配置(アライメント) の 得点で重み付けをする。
\[\begin{aligned} \mathbf{c}_t &= \sum_{i=1}^n \alpha_{t,i} \mathbf{h}_i & \text{ 出力のための文脈ベクトル }y_t\\ \alpha_{t,i} &= \text{align}(y_t, x_i) & \text{ 2 つの単語 }y_t\text{ 及び }x_i\text{ を配 置}\\ &= \frac{\exp(\text{score}(\mathbf{s}_{t-1}, \mathbf{h}_i))}{\sum_{i'=1}^n \exp(\text{score}(\mathbf{s}_{t- 1}, \mathbf{h}_{i'}))} & \text{ アラインメント得点のソフトマックス} \end{aligned}\]アラインメント関数
アライメントモデルは,位置 $i$ の入力と位置$t$ の出力の対 $(y_t, x_i)$ に,それらがどれだけ一致しているかに基づいて得点 $\alpha_{t,i}$ を付与する。 $\alpha_{t,i}$ の集合は,各出力に対して各ソース中間層状態をどの程度考慮すべきかを定義する重みである。 Bahdanau 論文では,アライメント得点 $\alpha$ は単一の中間層を持つフィードフォワードネットワークによって計量化され,このネットワークはモデルの他の部分と同時に学習される。 得点関数は,非線形活性化関数として $\tanh$ が使用されていることを考えると,以下のような形となる: \(\text{score}(\mathbf{s}_t, \mathbf{h}_i) = \mathbf{v}_a^\top \tanh(\mathbf{W}_a\left[\mathbf{s}_t; \mathbf{ h}_i\right])\)
ここで,$\mathbf{v}_a$ と $\mathbf{W}_a$ は共にアライメントモデルで学習される重み行列。
Building block モデルごとの性能
右: LSTM の概念図 (浅川2015)
- SRN without 注意以外のモデルでは,学習が可能であることが分かる。
- このことから,注意成分と RNN 成分とで,いずれが speech errors に関連しているのかを見定めたい,というリサーチクエスチョンが提起できる。本発表では,このことに焦点を当てた。
実験
入出力表現
- 入出力語彙辞書 (48 トークン): [‘
', ' ', ' ', ' ', 'N', 'a', 'a:', 'e', 'e:', 'i', 'i:', 'i::', 'o', 'o:', 'o::', 'u', 'u:', 'b', 'by', 'ch', 'd', 'dy', 'f', 'g', 'gy', 'h', 'hy', 'j', 'k', 'ky', 'm', 'my', 'n', 'ny', 'p', 'py', 'q', 'r', 'ry', 's', 'sh', 't', 'ts', 'w', 'y', 'z', 'ty', ‘:’] : 埋め草, : 語尾, :語頭, : 未定義をあらwす特殊トークン - 中間層素子数: 64
- 語末特殊トークン
を出力した時点で終了。 - 復号化器の中間層初期値 = 符号化器の終了時点の中間層状態
- 復号化器には注意機構を実装 such as chatGPT, BERT, and more.
中間層に加えた3つの処理過程
モデル0 全てのパラメータを微調整
モデル1 注意機構を固定して,GRU 側を微調整 水色: 運動計画と聴覚フィードバック制御 (カルマンフィルタ (Kalman1960) 様の制御を実現)
モデル2 GRU 側を固定して,注意を微調整 青:トップダウン注意
赤色:エンコーダの出力. 音素系列,ボトムアップ注意,言いたい事:固定 like a STM (Baddley1992)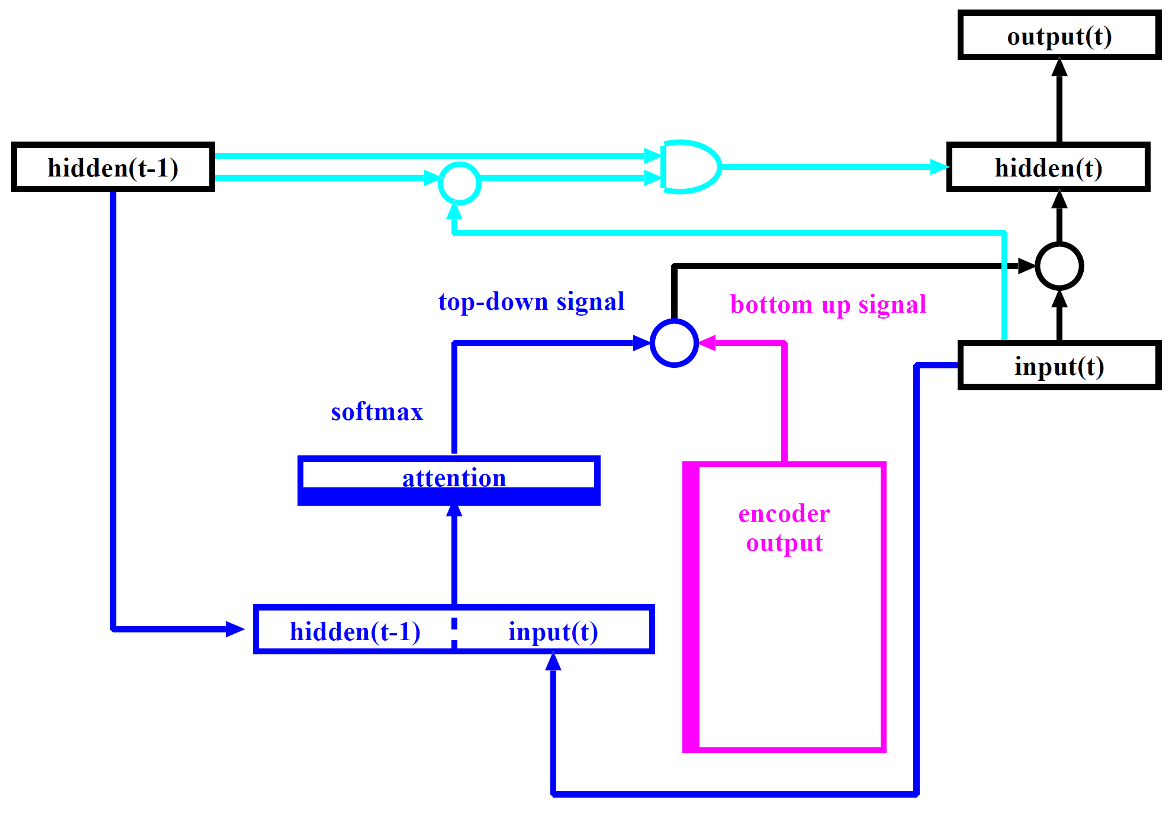
事前学習と微調整
- 事前学習 pretraining : 健常モデルとみなす。
- 転移学習 transfer learning と微調整 fine tuning:
- 転移学習: 最終層と最終直下層との結合のみ再学習
- 微調整: すべての層の結合を再学習
-
転移学習,微調整完了後のモデルを実際の言い誤り生成器と見なす。
- 健常者であれば,時間的,精神的ストレスのかかった状態での発話場面
- 失語症,難読症であれば言い誤りに現れる機能変化
上記をモデルのパラメータ変容によって説明可能か? (ボクセル障害マッピング Dronkers+ などから触発され着想
結果
一旦,通常の単語の発話を学習したモデルに対して,提案モデルにおいて,水色部分と青色部分の両者とも微調整対象にした。 結果は,ほとんど全ての言い誤りを再生させることができた。
- 実際には,刺激「ノートルダム」については,2 つの正解が存在する(ノートムダルとノールトダム)。
-
このため,微調整では,このノートルダムの言い間違えの 1 つについてのみ,言い間違えに失敗し,143/144 の言い間違え率を得た。
- モデル 0: 全体を微調整
-
モデル 1: モデルの水色部分のみ微調整を行い,青色部分を固定した場合
96.5% の言い間違えを再現した。言い間違えに失敗した例は,「たのしませて」(実際の言い間違え例はタノマシ)を/タノシャシ/ などであった。
-
モデル 2: 一方,水色部分を固定して微調整を行う
言い間違え再現率は 52/144 = 36.11 % であった。
このことから,成人の言い間違えデータの生成源は,水色部分,すなわち,音の運動出力の繋がり部分の不具合に起因し,語彙的表象の変容だけでは,36 % 程度しか再現できないと言えるだろう。
その他のエンコーダ・デコーダモデル
その他 1. 三角モデル (近藤・伊集院・浅川2023)
- O(rthgraphy), P(honology), S(emnatics) のそれぞれに対して,ソースとターゲットと見立てた,9 つのデータセット,モデルを用意
モデル名を下表に示す。 表中の x2y は,ソースが x [o,p,s] でターゲットが y [o,p,s] であるモデルを意味する。 カッコ内は,ソースとターゲットのそれぞれが,系列データであれば Seq であり,埋め込みベクトルデータであれば Vec である。
| source\target | O | P | S |
|---|---|---|---|
| O | o2o (Seq2seq) | o2p (Seq2Seq) | o2s (Seq2Vec) |
| P | p2o (Seq2Seq) | p2p (Seq2Seq) | p2s (Seq2Vec) |
| S | s2o (Vec2Seq) | s2p (Vec2Seq) | s2s (Vec2Vec) |
ソースからターゲットへと系列データかベクトル埋め込みデータかによって,モデルは 4 種類に分類できる。
- 系列から系列へ: 4 (o2o, o2p, p2o, p2p),
- 系列からベクトル埋め込みへ: 2 (o2s, p2s)
- ベクトル埋め込みから系列へ: 2 (s2o, s2p)
- ベクトル埋め込みからベクトル埋め込み 1
その他 2. オノマトペ生成器 (橋本・浅川 準備中)
オノマトペ 小野+2007 「日本語オノマトペ辞典」の 4500 オノマトペから,word2vec にエントリのある 1741 語を用いて上記の三角モデルの枠組みを用いた
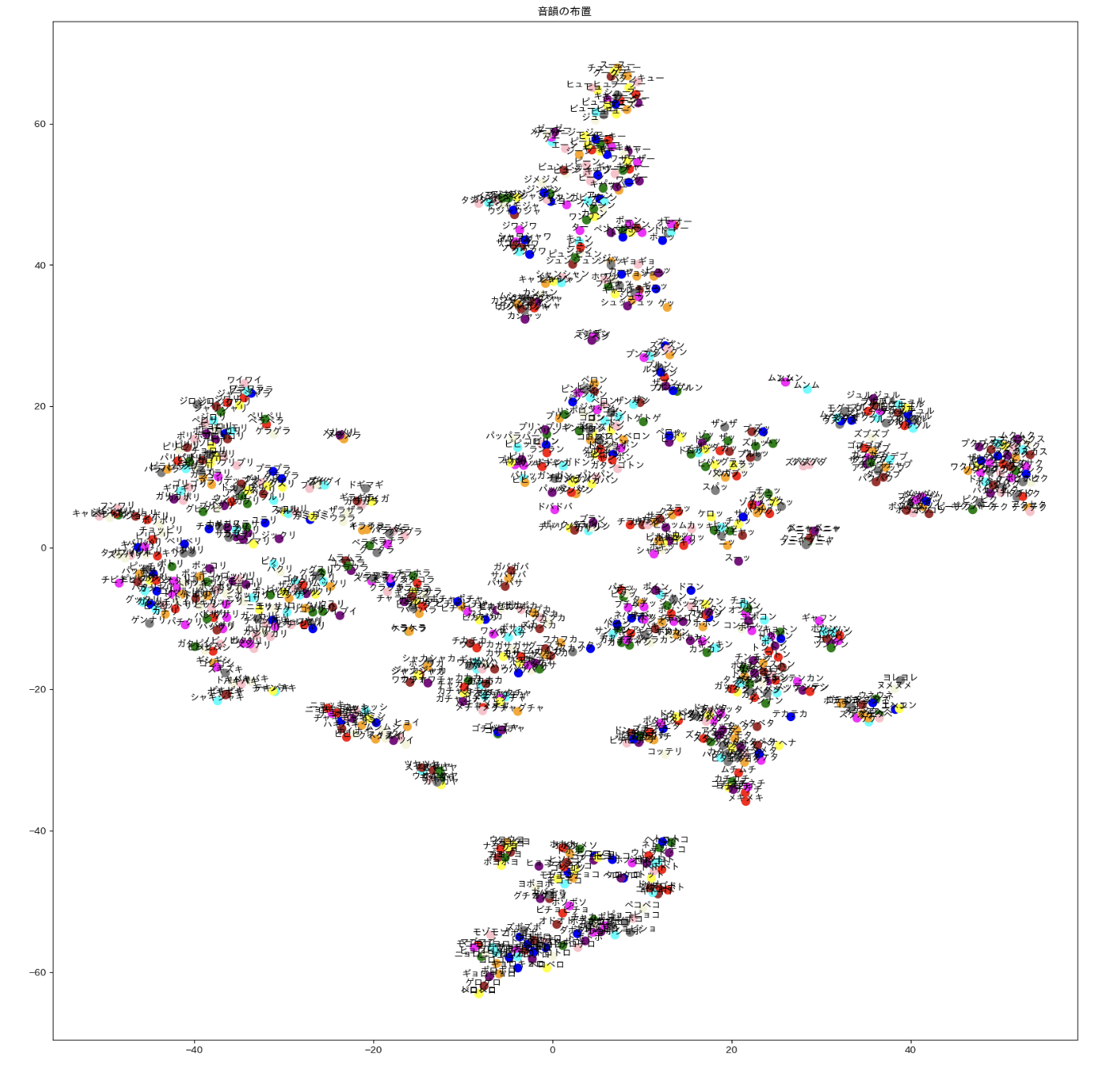
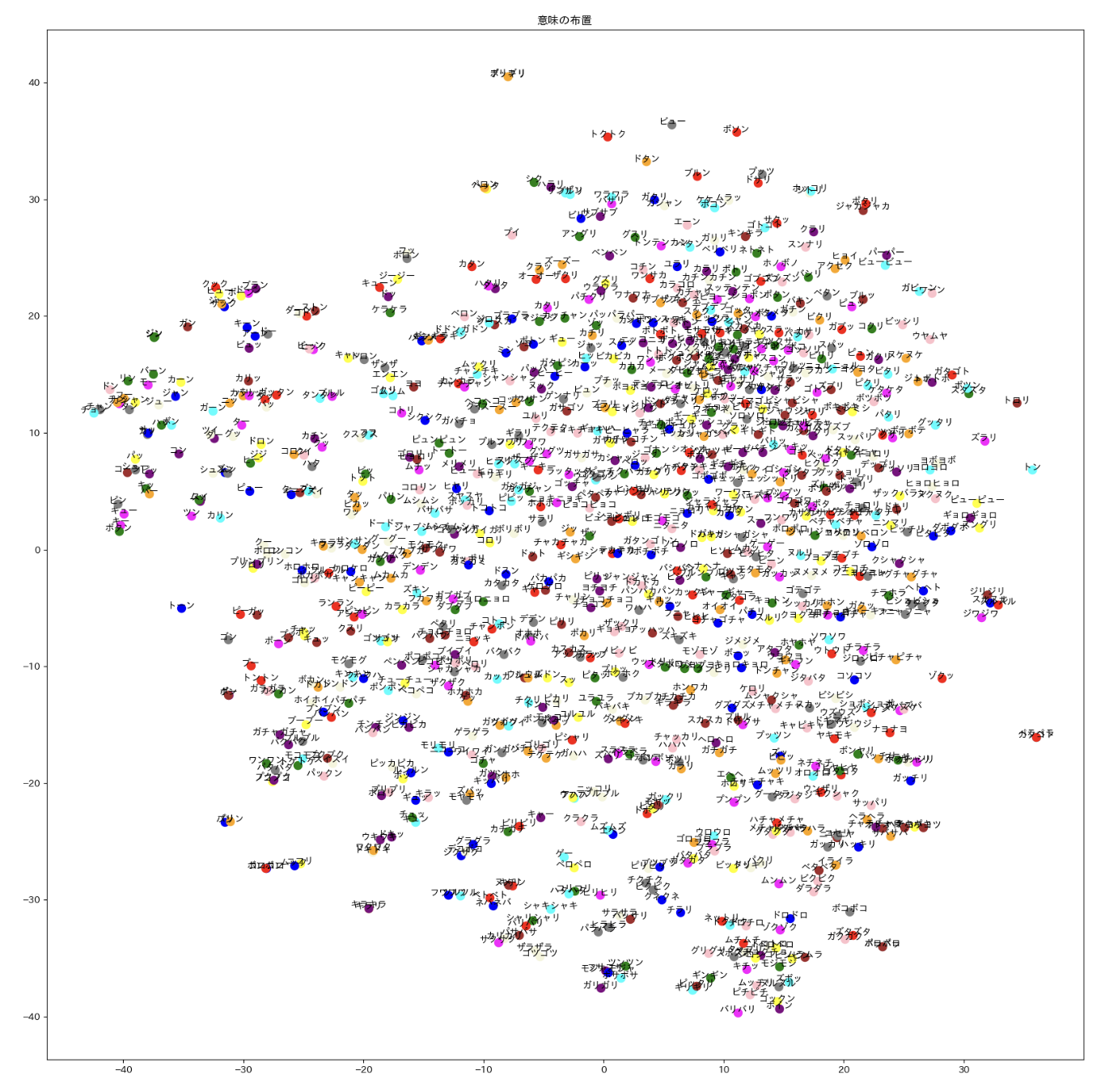
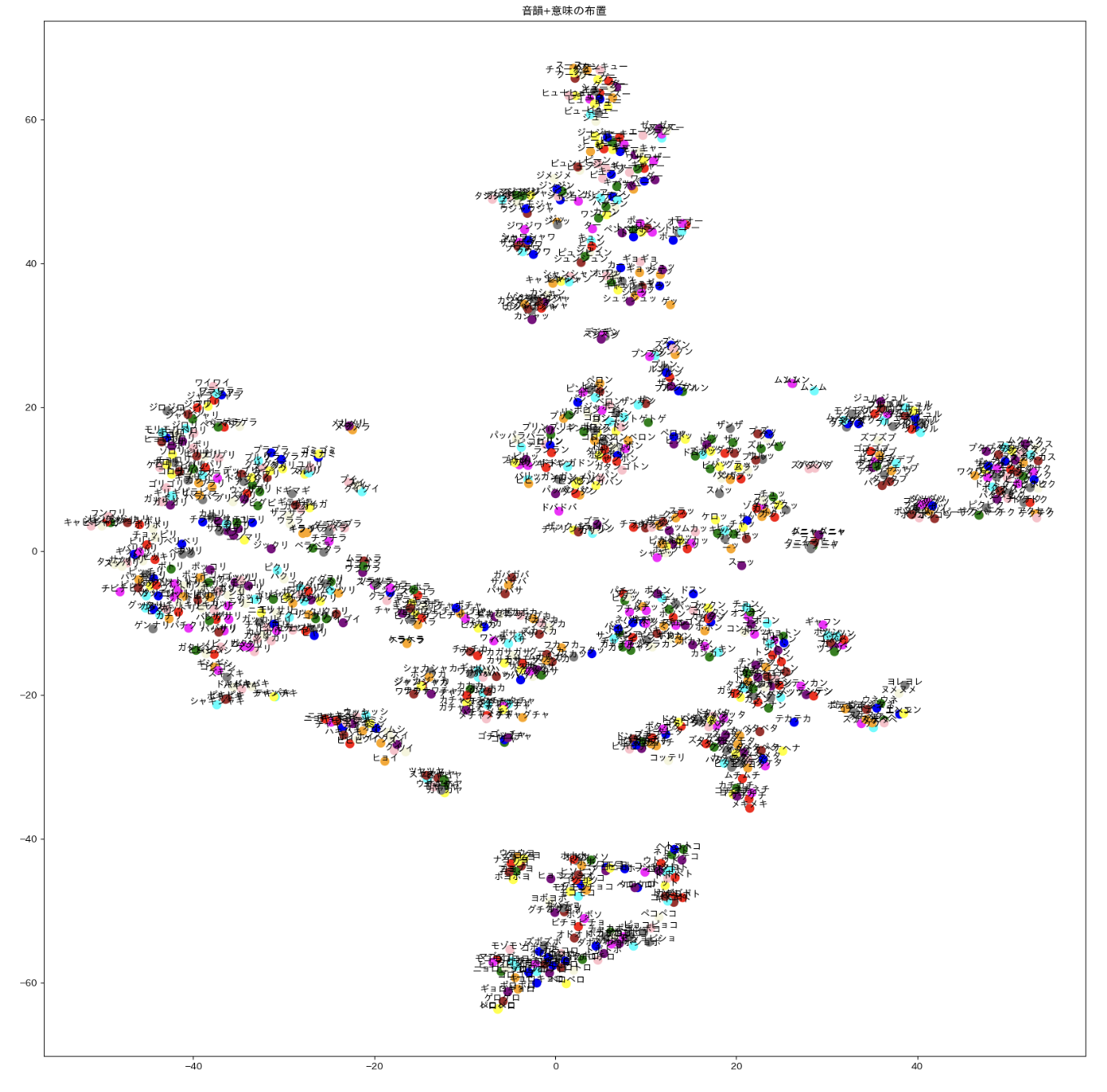
中: 対応するオノマトペの word2vec データを tSNE を用いて視覚化
右: 音韻+意味 の混合表象を tSNE を用いて視覚化
その他 3. ストループ効果 (永田・浅川 準備中)
