DaSiC 7 (2023) Linguistics and Data Science in Collaboration 発表資料

Copyright (C) 2023 Shinichi Asakawa
Shin Aasakawa, all rights reserved.
https://opensource.org/license/mit/

実演 鏡を覗いてみると

怪物と戦うものは，自分もその怪物とならないように用心するがよい。 そして，君が長く深淵を覗き込むならば，深淵もまた君を覗き込む
146 (ニーチェ，木場深定訳，善悪の彼岸，120ページ，岩波書店)
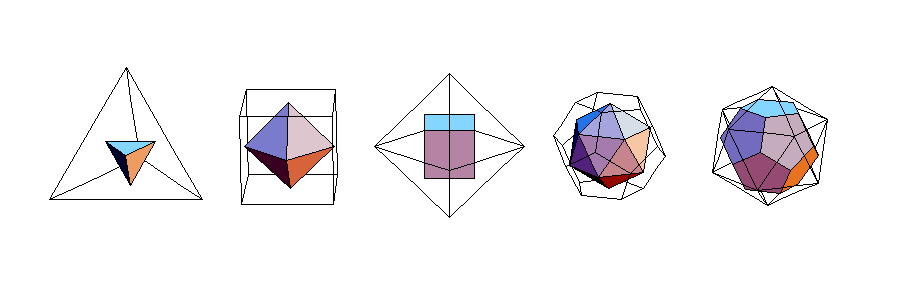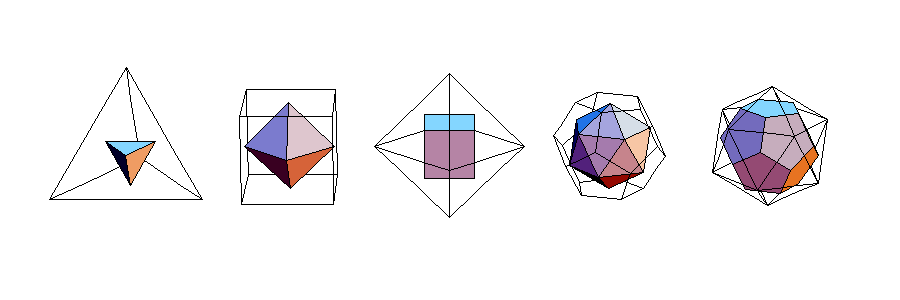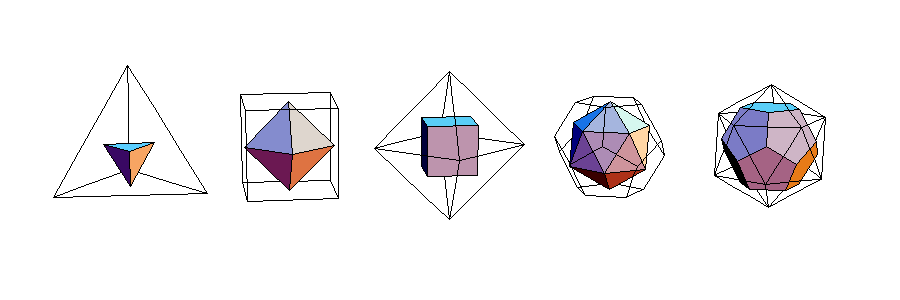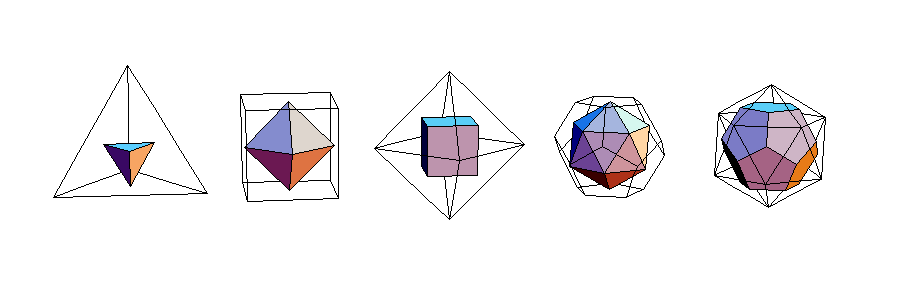
画像出典: [双対性](https://ds.cc.yamaguchi-u.ac.jp/~math/toybox/polyhedron_soral/explanation/037_4.html)
左から，正四面体，正六面体，正八面体，正十二面体，正二十面体

Table of contents: part 3 第三部目次 (16:25-17:40)

  1. ちはやふる Transformer を用いた符号化器・復号化器モデルによる百人一首
  2. ヨコ型，タテ型の言い誤りのシミュレーション Horizontal and vertical errors in speech errors

実習ファイル

0. 双対性 duality

機械学習，あるいは，最適化理論において，双対性 duality または双対性原理 duality principle とは，最適化問題を主問題 primal problem と双対問題 dual problem の 2 つの観点から見ることができることを指す。 主問題 primal problem が最小化問題であれば，双対問題 dual problem は最大化問題である (逆も同様)。 主問題 (最小化問題) に対するどのような実行可能解も，双対問題 (最大化問題) に対するどのような実行可能解も，少なくとも同じ大きさである。 したがって，原始問題の解は双対問題の解の上界であり，双対問題の解は主問題の解の下界である。この事実は弱双対性 weak duality と呼ばれる。

Lagrange 双対問題は，非負の Lagrange 乗数を用いて目的関数に制約を加えることによって最小化問題の Lagrangian を形成し，元の目的関数を最小化する主変数の値を解くことによって得られる。 この解法は，Lagrange 乗数の関数として主変数を与え，これを双対変数と呼ぶ。 従って，新しい問題は，双対変数に関する制約 (少なくとも非負制約を含む) の下で，双対変数に関して目的関数を最大化することである。 von Neumann によれば，双対問題と呼ばれる別の視点を用いることで，主問題または双対問題のどちらを解いても最適解が得られるという理論を概念化できる。

1. ちはやふる Transformer を用いた符号化器・復号化器モデルによる百人一首

1.1 Transformer, Attention is all you need

単語の多義性解消のために，あるいは単語のベクトル表現を超えて，より大きな意味単位である，句，節，文のベクトル表現を得る努力がなされてきた。 適切な普遍文表現ベクトルを得ることができれば，翻訳を含む多くの下流課題にとって有効だと考えられる。

そこで，注意機構を積極的に取り込んだゲームチェンジャーが Transformer である。

             
Transformer [2017Vaswani++](https://arxiv.org/abs/1706.03762) Fig.2 を改変

上図で，matmul は行列の積，scale は，平均 0 分散 1 への標準化，mask は 0 と 1 とで，データを制限すること，softmax はソフトマックス関数である。

1.2 Transformer における位置符号化器 (PE: position encoders)

\[\text{PE}_{(\text{pos},2i)} = \sin\left(\frac{\text{pos}}{10000^{\frac{2i}{d_{\mathop{model}}}}}\right)\] \[\mathop{PE}_{(\mathop{pos},2i+1)} = \cos\left(\frac{\mathop{pos}}{10000^{\frac{2i}{d_{\mathop{model}}}}}\right)\]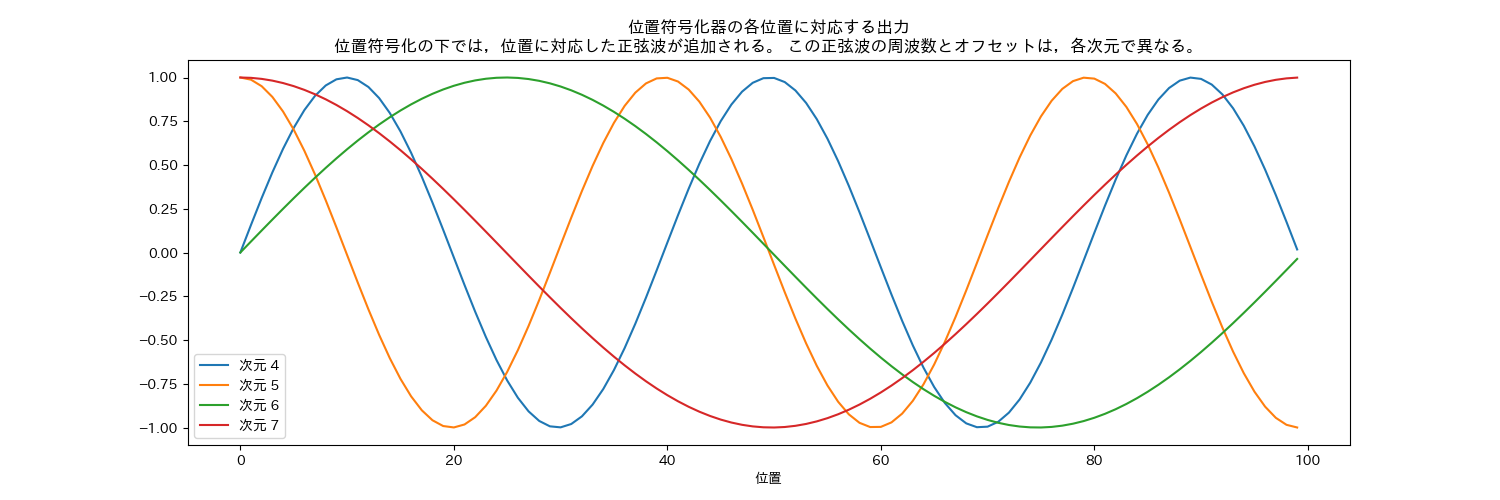
Transformer の位置符号化器の出力。 Transformer は位置情報を持たないので，位置情報を周波数変換して用いる。

1.3 事前訓練

マスク化言語モデル

次文予測課題

言語モデルの欠点を補完する目的，次の文を予測

[SEP] トークンで区切られた 2 文入力

ファインチューニング GLUE 課題 (General Language Understanding Evaluation)

1.4 Transformer (SBERT) の文ベクトル

先に紹介した word2vec は，単語ベクトルを得る手法であるが，Transformer は文ベクトルを扱う。 そこで，文単位での類似性を検討した。 下の画像に対して，5 つの脚注がある。


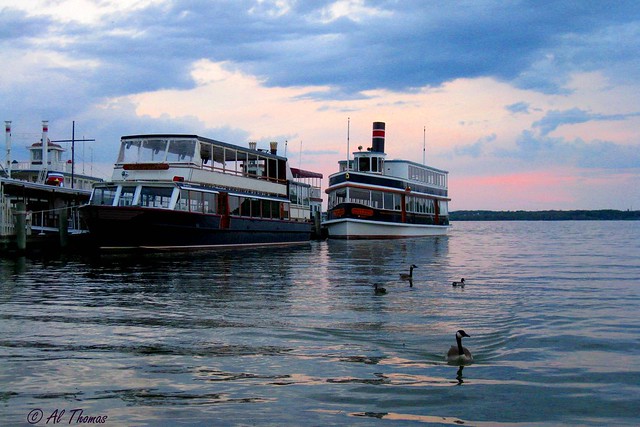
  1. 夕暮れのハーバーに汽船と複数の鳥が浮かんでいる
  2. 水面に浮かぶ4羽の水鳥と、その向こうに停泊している2隻の船
  3. 船着き場に2艘の船がとまっている
  4. 朝焼けの中待機場所にある旅客船とマガモ
  5. 停められた船の近くで水鳥が泳いでいる
    MS COCO データセットより: http://farm5.staticflickr.com/4055/4704393899_a041476b4a_z.jpg

上図は，MS COCO 画像データと画像に対応する脚注からなるデータセットからの一例である。 日本語文は，千葉工業大学 STAIRLABO が公開しているデータである。 人間が見れば，写真と文章とは結びいていることが分かる。 加えて，5 つの脚注も相互に似ていることが分かる。 MS COCO データセットでは，一枚の写真に 5 つの脚注が紐付けられている。

コンピュータにこれらの文章が似ていることを判断させようとすると，最近まで難しい仕事であった。 本章で紹介する，文の意味ベクトルを用いると，これらの文章が相互に似ていると判断させることが可能である。 下図は tSNE を用いて，日本語の文章の類似度を sentence BERT を用いて表現し，文章の類似度に従って地図を描いたものである。 図では，同じ写真に紐付いている文章は同じ色で表現している。

1.3 性能評価 intstructGPT (a.k.a chatGPT)

図 3.13: ニュース記事がモデルによって生成されたものであるかどうかを識別する人間の能力 (正しい割り当てと中立でない割り当ての比率で測定) は，モデルサイズが大きくなるほど低下する。 意図的に悪い対照モデル (出力のランダム性が高い無条件 GPT-3 小型モデル) の出力に対する精度を上部の破線で示し，ランダムな確率 (50 %) を下部の破線で示す。ベストフィットの線は 95 %信頼区間を持つべき乗則である。 [Brown+2020](https://arXiv.org/abs/2005.14165) Fig. 3

1.4 結果

エポック 4 終了時のエラーは以下のとおり：

百人一首 上句をエンコーダに与えて，下句をデコーダに予測させた結果。3 エポック目の出力を示す。 青は正解文字，赤は，誤りを示す。旧かなである `ゐ` を間違えるのは，低頻度である可能性が考えられる。

2. ヨコ型，タテ型の言い誤りのシミュレーション

2.1 モデル

2.2 結果

一見すると，タテ型の言い間違えの方が再現できていないように見えますが，学習語彙に含まれない語彙が多いという理由かも知れない。 ヨコ型の再現失敗例を以下に示す:

出力 言い誤り 文 入力 意図 文
足の筋肉は収縮すると、もう足の、非常にいろんな点でね、足の[UNK]環を良くしますし 入力文:足の筋肉は収縮すると、もう足の、非常にいろんな点でね、血液の循環を良くしますし
出力文:このアブラムシがいわゆる寄生しますとね、アブラカスの分[UNK]物をね… 入力文:このアブラムシがいわゆる寄生しますとね、アブラムシの分泌物をね…
出力文:重傷の火傷はね、皮[UNK]が無いために水分が出てしまって、タンパク質が出てしまって、非常に重傷になるわけです 入力文:重傷の火傷はね、皮膚が無いために水分が出てしまって、タンパク質が出てしまって、非常に危険になるわけです

以上がヨコ型言い間違え，再現失敗例の全てであった。

一方，タテ型言い間違え再現失敗例は以下のようになった:

出力 言い誤り 文 入力 意図 文
ロンドン、ボストンていう便はさ… ロサンゼルス、ボストンていう便はさ…
御前崎、波は2メートル、うなりは不明 御前崎、波は2メートル、うねりは不明
今日[UNK]枚組のタオルを 今日のプレゼントクイズはこの６枚組のタイルを
大相撲初場所[UNK]日目千秋楽の一番 大相撲初場所６日目結びの一番
水戸三高[UNK]年生、なかなかスケールのおおいランナーです 水戸三高の３年生、なかなかスケールのおおきいランナーです
広島ノー・[UNK]、[UNK]塁というピンチをつかんだんですが 広島ノー・アウト２、３塁というチャンスをつかんだんですが
乾[UNK]して砂が浮いてきた 乾燥して石が浮いてきた
さんと長谷川[UNK]点[UNK]点で同意語で さんと長谷川さんが７点と７点で同同点で
[UNK]年から国の政治としてとりいれられた ４８年から国の制度としてとりいれられた
[UNK]通くらい募集があったというけれども、応募かね ７０通くらい応募があったというけれども
ゲームは第[UNK]入ってジェッツの攻撃 ゲームは第２クォーターに入ってジェッツの攻撃
[UNK]回ワンナウト、これでゲームあったかにみえましたが ９回ワンナウト、これで勝負あったかにみえましたが
[UNK]、[UNK]塁、一人はシングルヒット、もう一人はデッドボールを選んで塁に出ています ランナー１、２塁、一人はシングルヒット、もう一人はフォアボールを選んで塁に出ています
[UNK]年までに、あの水準まで、あの、とどけようと ５９年までに、あの水準まで、あの、到達しようと
歌舞[UNK]なんかでね、主人公がやせていたらこれはえになんない 歌舞伎なんかでね、主人公がやせていたらこれは芝居になんない
[UNK]日目まで優勝 ５日目まで全勝
[UNK]子をコの字形に並べて 机をコの字形に並べて
この方は明治[UNK]年代の御出身で この方は明治４０年代のお生まれで
[UNK]角度で ４５メートルの高さで
[UNK]年の民社党の分裂とかですね ３５年の民社党の独立とかですね

文中の [UNK] は，そもそも学習語彙中に存在しないので，学習しようがない。 [UNK] トークンの問題を考慮すれば，タテ型の言い誤りも，再現できているように思われる。

3. 考察

ここまでをまとめると以下のようになる:

3.1 制約項からみた定式化

機械学習における目的関数 (損失関数) は次式で与えられる:

\[\tag{一般形} \text{目的関数} = \text{誤差} + \lambda\left(\text{正則化項}\right)\]

ここで，$\lambda$ は Lagrange 乗数である。

word2vec においては，

\[\tag{word2vec} \text{目的関数} = \text{標的単語との誤差} + \lambda\left(\text{負事例 ただし ランダムにサンプリング}\right)\]

で与えられていた。 Dell モデルのパラメータ推定においては，次式となる:

\[\tag{Dell model} \text{目的関数} = \text{単語カテゴリ確率との誤差} + \lambda_{1}\left(\text{s,p パラメータへの制約}\right) + \lambda_{2}\left(\text{w,d パラメータへの制約}\right) + \lambda_{3}\left(\text{温度パラメータ $\beta$ への制約}\right)\]

一方，エンコーダ・デコーダモデルにより言い間違えのシミュレーションでは，次式で与えられる:

\[\tag{speech errors} \text{目的関数} = \text{正しい単語と言い間違え単語との誤差} + \lambda_{1}\left(\text{注意機構への制約}\right) + \lambda_{2}\left(\text{フィードバック機構への制約}\right)\]

同様にして，タテ型，ヨコ型の言い間違え Transformer モデルでは，次式を用いた:

\[\tag{speech errors Transformer 1} \text{目的関数} = \text{正しい文と言い間違え文との誤差} + \lambda_{1}\left(\text{ヨコ型言い間違えに対する制約}\right)\] \[\tag{speech errors Transformer 2} \text{目的関数} = \text{正しい文と言い間違え文との誤差} + \lambda_{1}\left(\text{タテ型言い間違えに対する制約}\right)\]

式 (speech errors Transformer 1) と 式 (speech errors Transformer 2) との関連は，現在のところ不明である。 しかし，本モデルでは，文法知識の制約，例えば Dell+2008 のごとき 構文的交通巡査 (traffic cop) のような機構を仮定しなかった。 むしろ Transformer による本モデルでは，文法的，統語的な規則を明示的に記述せず，訓練コーパスの学習を通じて，ニューラルネットワークのアーキテクチャと結合係数へと反映された点に留意スべきである。

4. 議論 ありえない有能さ Unreasonable effectiveness

Lagrange 乗数を，変分問題として定式化し，制約項に対する意味付けを考えるアプローチは，物理学で始められた。 制約付き最適化は，画像復元においては 標準正則化理論 (Poggio+1985) で定式化された。 機械学習においては，汎化性能向上のための制約と考えられてきた。 近年では，目的関数とと制約項と与え方を検討することで，GAN や stable diffusion 等の生成 AI でも用いられている。

変分 Bayes の考え方でも同様であり，目的関数を Lagrange 方程式とみなせば，目的関数 (主問題) の最小化問題を，制約項付き双対問題の最大化ととらえうる。 このようにして，他分野で提唱された概念を，援用することで現象を見通しよく説明できる。 補足資料 変分問題と標準正則化 も参照のこと。

主張 Takeaways (再) まとめ

  1. 大規模言語モデル (LLM)，一般画像錦 (ImageNet) で事前訓練されたモデルに対して，転移学習 transfer learning を行うことで，関心領域の課題を解くモデルを作成
  2. 関心課題に特化したモデルに対して，任意の条件とデータとを用いて，微調整 fine-tuning を行うことで，条件間の差異や生成機序を解明。
  3. モデル，データ，パラメータ の三項は，言語学的規範，行動・臨床データ，機械学習モデルの三項と連結。微調整に用いる条件は，制約条件付き最適化 constrained optimization とみなしうる。このことは，データサイエンスにおける，モデルとパラメータの関する双対性原理 duality principle として定式化

キーワード keywords

符号化・復号化モデル，転移学習，微調整，トランスフォーマー，注意，ソフトマックス，ワンホットベクトル, 埋め込み表現，ラグランジェ双対性
Encoder-decoder models, Transfer learning, Fine-tuning, Transformer, Attention, Softmax, onehot vector, Embeddings, Lagrange duality,

Project CCAP