キーワード: 絵画命名課題, 相互活性化モデル, パラメータ推定, ソフトマックス関数, ワンホット表現, ボルツマン分布, 温度パラメータ
keywords: Picture naming tasks, the Interactive Activation model, parameter estimation, softmax function, one-hot expression, Boltzmann distribution, thermal parameter
たとえば，よくある以下のような既述のうち，一部だけ再現するモデルに意味があるのだろうか。
症例 B は 60 代の右利き女性。自発話は，構音障害や発語失行はなく流暢で，喚語困難による停滞はあるが錯語はほとんど認められず，指示代名詞の多い空虚な発話だった。 声量・発話速度・発話量は普通だった。 初診時（発症1 ヵ月）のSLTA では，呼称 25％ と喚語困難が重篤で，聴理解は単語 90％ と単語レベルから誤りがあった。 復唱は単語 80％ で音韻性錯語を認め，音読も漢字単語 60％，仮名単語 80％ と低下していた。 文字理解は音声と同程度に低下し，書字は漢字・仮名文字とも困難だった。
4 つの理論的立場を表す模式図。 太い矢印はターゲットに関わる活性化の流れを、細い矢印はその語彙の近傍に関わる活性化の流れを、そして輪郭のある矢印は前に描かれた理論に対して追加または変更された活性化の流れを示す。
活性化とフィードバックのカスケードの結果。
絵画命名課題を説明する従来の IA モデルの持つ問題点を取り上げ，その簡便法を提案する。 従来手法では，結果を検討するための web インターフェイスが用意されているものの，ハイパーパラメータが固定されていた。 このため，シミュレーション結果を解釈することが容易でなかった。 本稿に示す提案手法に従えば，従来手法では調整が困難であったパラメータの検討が容易になる。
絵画命名課題は，計算論的臨床失語症プロジェクトの中心課題の一つである。 言語関連の認知神経心理学課題の中で，視覚入力を音声出力へと変換する課題は， 記憶や注意などの，高次認知機能とは独立に計測可能だと考えられてきたこと， 関連する認知心理学モデル (パンデモニアム(Selfridge 1958) やロゴジェンモデル(Morton 1969) など) と親和することから多くの研究がなされてきた。 1980 年代に提唱された相互活性化モデル (以下 IA)(McClelland and Rumelhart 1981) に基づいて，絵画命名課題を説明するモデルである 2 段階相互活性化モデル(Dell 1988) は，それらの中の代表的な一モデルとなっている。 本稿では IA モデルの改良を試みた。 取り上げたモデルは 二段階相互活性化モデル e.g. Levelt(Levelt 1989), Dell(Dell 1986), Roelofs(Roelofs 1992) に基づくものである。
本発表では，絵画命名課題 (PNT: Picture Naming Tasks) のためのシミュレーションモデルを取り上げた。 代表的なモデルとしては，Dell (Dell et al. 1997, 2000Foygell_Dell_SP; 2004) のモデルである。 広義には Levelt, Roelofs らの WEAVER とその後継モデル(Roelofs 1997, 2005, 2014; Levelt, Roelofs, and Meyer 1999) を含む。
PNT は刺激図版を視覚入力として，対応する単語を産出するまでの心的機構を扱っている。 だが，第 2 次ニューロブーム中の計算資源や理論的な問題が指摘でき，現代的な視点からすれば，改善の余地がある。
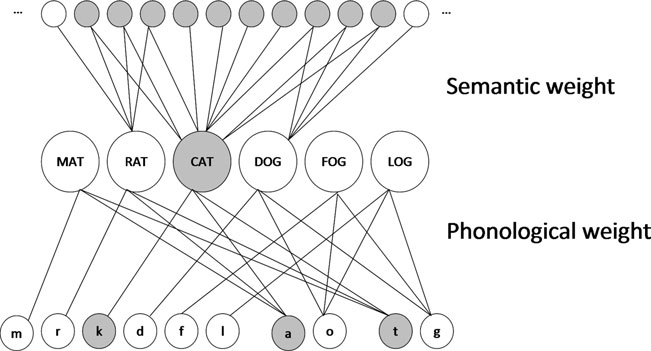
図 1 従来モデルの概観。左: IA （Dell, 1997; Foygell & Dell, 2000) モデル， 右: WEAVER++/ARC モデル。Roelofs (2020) Fig. 1 を改変。
20 年以上の伝統のあるモデルであるが，現代的な視点からは問題点が指摘できる。
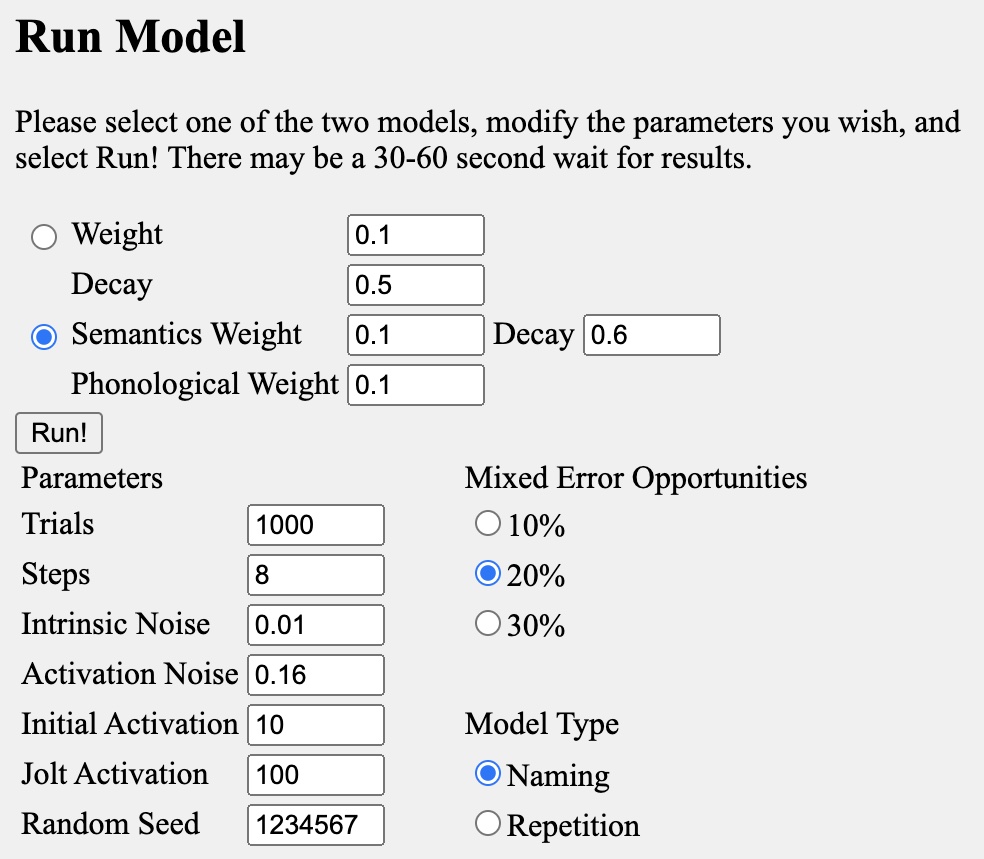
図 2 結果の確認サイト (http://langprod.cogsci.illinois.edu/cgi-bin/webfit.cgi) のスクリーンショット。 左: データ適合のためのインターフェイス。パラメータは固定。 右: パラメータを変動させて挙動を確認するインターフェイス。 残念ながら，右図で変動させたパラメータを反映させて，左図で確認する手段は提供されていない。 そのため，左図でのモデル推定は，予め定められた固定のパラメータで実行した結果を検討することしかできない。
上図に沿って，Dell の IA モデルに用いられるパラメータを概説する。 上図左は，SP, WD 両モデルで用いられるパラメータ推定のための web インターフェイスである。 ユーザは，6 つの反応カテゴリに各反応頻度，あるいは回数を入力し，続けて Fit! ボタンを押すことで，パラメータを推定することができる。
右図中段に書かれているとおり，非単語欄に数値を入力して実行すると，2004 年の論文で遡上に挙げられた，語彙-編集モデルとなる。 一方，全欄に数値を入力して実行すると，独立あるいはしきい値モデルに相当することとなる。
一方，上図右は，推定に用いられるハイパーパラメータを変化させるために用いられる。 図に示されている数字は，右図の入力である 6 つの反応カテゴリーの割合を生じさせるために用いられる。 すなわち，右図は，左図のパラメータ，とりわけ，左図上部の 4 パラメータを探索する目的で使用される。 一方，左図のパラメータを定めると右図の入力である 6 つの反応カテゴリーの比率が生じることとなる。 従って，左右の図は，互いにその数値の発生因となるという相互活性化の関係にある。
上図左に示された数値は，機械学習でいうハイパーパラメータに相当する。 モデルの動作に影響を与えるパラメータであるが，オリジナルのモデルでは固定されていると推察される。 ここで，次のような疑問を上げることが可能である。
モデル中の任意のニューロン \(a\) の活性値は次式で与えられる: \[ a_{i,t+1} = (1-d) a_{i,t} + w \sum_{i\ne j} a_{j,t} + \text{Noise} \]
Dell モデルでは，ノイズには 2 つの成分がある。 すなわち，上式右辺最終項で Noise とは，2 つの正規分布からなる。 これらの明示的に式に表現すれば次式を得る:
\[ a_{i,t+1} = (1-d) \left(a_{i,t} \left(1+\mathcal{N}(0,0.4^2)\right)\right) + w \sum_{i\ne j} a_{j,t} + \mathcal{N}(0,0.1^2) \]
IA モデルでは上層が入力層である意味入力，中が語彙層，下が音素を表現している。 典型的な場合のニューロン数は入力層が 57，中間層が 6, 出力層が 32 である。 中間層の 6 つはそれぞれの 語彙，またはレンマを表現している。 具体的には cat, dog, mat, rat, mat, log である。 ミューレションでは，入力刺激は，常に 1 種類しか存在しない。 すなわち入力は常に ネコ を表す意味ベクトルである。 このため，175 回ネコを見せられていることに相当する。 正解であるネコの意味ベクトル入力に対して，cat を発話すれば，正解，dog を発話すれば，意味エラー semantic errors と解釈される。 同様にして，出力が mat なら 形態エラー formal errors, rat なら 混合エラー mixed errors, mat なら 無関連エラー unrelated errors, log なら 非単語 non-word errors あるいは 新造語エラー，とみなされる。 フィラデルフィア絵画命名検査 PNT(Roach et al. 1996) では 175 枚の刺激図版が個別に被検査者に提示される。 PNT では，各図版を逐次被検査者に提示し，図版に描かれた内容を口頭で答えることが求められる。 ところが，シミュレーション研究では，上のネットワークが用いられている。 すなわち，IA モデルによる絵画命名課題のシミュレーションでは，ネコ画像を 175 回提示して，どの種のエラーが報告されたかを計数している。 初期のモデルは 1980 年代に提案された オモチャ toy モデル であったことを斟酌しても，現代的な意味ではおもちゃにすぎるほど拙く幼稚なモデルであるとの誹りを免れない。 失語症検査では現実世界の多様な内容を可能な限り汲み取ることを意図して，多様な図版が用いられる。 そのような図版から，失語症の多様な病態を把握することが失語症検査の要件であると推察される。 駄菓子菓子，驚くべきことに 2019年 に公刊された論文，例えば (Roelofs 2019) であっても，中間層の語彙層数は 6 ニューロンに限定されたままである。 検査に使用される図版は，被検査者の言語機能を調べる目的で広範な題材から選ばれたものであることから， それぞれの図版をその都度評価することで現実的なモデルに近づけることが可能となると考えられる。 このことから，本稿では実際の図版をモ入力画像として，ニューラルネットワークモデルを訓練することとした。 実際の失語検査で用いられる図版を入力刺激とし，対応する正解を口頭出力するまでをモデル化した。 訓練済モデルを健常者モデルとし，健常者モデルの一部パラメータを変更することで失語症モデルとみなすこととした。
患者に対して絵画命名検査を実施して得られた臨床データを教師データとして，モデルを既述パラメータを勾配降下法によって求めることを提案する。 Dell らのモデルとの対応では，\(s, p\) または \(w, d\) が探索すべきパラメータである。 SP モデルでは \(d\) は固定であり，WD モデルでは \(s=p=w\) である。 提案モデルでは，これら 4 つのパラメータ \(\{s,p,w,d\}\) を推定することを試みた。 このとき \(s\ne p\) であれば，SP モデルを近似することになり，一方 \(s\simeq p\) であれば WP モデルを近似することになる。 Dell は，SP と WD 両モデルの比較に関心があったため，両モデルでパラメータ数を揃える必要から，モデルのパラメータ数に制約を置いたと推察される。 2 つのモデルだけが存在し，かつ，これら 2 つのモデルのうちどちらかが正しいことが保証されるという事態を想定することは難しいと考える。 なぜなら，相互活性化モデルでは \(s\) の低下を \(p\) が補うなど (\(w,d\) についても同様) 補完関係が想定できるからである。 また，ある種の患者のリハビリテーションによる機能代替や，失われた機能の代替的回復モデルなどを考慮すれば，異なる組み合わせのパラメータ集合が同一の結果を生じる可能性が否定できないからである。
そこで本稿では，SP モデルか WD モデルかという，モデル間の比較には立ち入らず，パラメータ推定問題と捉えることとした。 従って，推定すべきパラメータは \(\theta=\{s,p,w\}\) である。 各反応カテゴリーの生起確率は，ソフトマックス関数に従う確率密度関数に従うと仮定する。 従って，カテゴリ \(x_i\) の生起する確率は次式で与えられる:
\[ p(x_i;\beta) = \frac{\exp\left(f(x_i)/\beta\right)}{\sum_j \exp\left(f(x_j)/\beta\right)}, \] ここで，\(f(x_i)\) は \(i\) 番目の反応カテゴリの音韻ユニットの出力である。 \(\beta\) は統計力学からの類推から温度パラメータと呼ぶことにする。 ソフトマックス関数は，統計力学におけるボルツマン分布と同一であって，\(x_i\) のエネルギー順位を与える式である。 このとき，\(\lim\beta\rightarrow0\) の極限では系は決定論的に振る舞い，\(\lim\beta\rightarrow\infty\) ではあらゆるエネルギー準位をとることとなる。 温度パラメータの導入意図は，このように系が確率的変動を許容する程度を表すものと解釈できる。 絵画命名課題において，健常者は \(\beta\) が小さい，従って温度低く安定した反応を生じることに対応する。 一方，反応が検査の都度変動するような，ある種の患者の回答は，温度パラメータ \(\beta\) が大きい，従って温度が高いとみなしうる。
ソフトマックス関数は，ニューラルネットワークで分類課題に用いられている意味で汎用性が高い。 また相互活性化モデルの確率論的改訂である多項相互活性化モデル MIA (Multinomial Interactive Activation) モデル(McClelland 2013; McClelland et al. 2014) でも類似の概念が用いられている。 すなわち，本稿で提案するモデルは，オリジナルの IA モデルを拡張した MIA モデルの概念を援用して， 絵画命名課題の妥当な解釈を行っているものとみなしうる。 ただし， MIA モデルでは，温度概念を推定すべきパラメータとして扱っていない。 温度パラメータ \(\beta\) を反応の安定性，あるいは多様性をとみなす考え方は，本稿独自のものである。
また，ソフトマックス関数に温度パラメータを導入するアイデアは，ボルツマンマシン(Ackley, Hinton, and Sejnowski 1985; Hinton and Sejnowski 1986) からの伝統である。 加えて，近年精度向上が著しい深層学習分野での自己半教師あり学習 (Self semi-suupervised learning) でも採用されている概念でもある(Oord, Li, and Vinyals 2018; Jaiswal et al. 2020; Chen et al. 2020)。
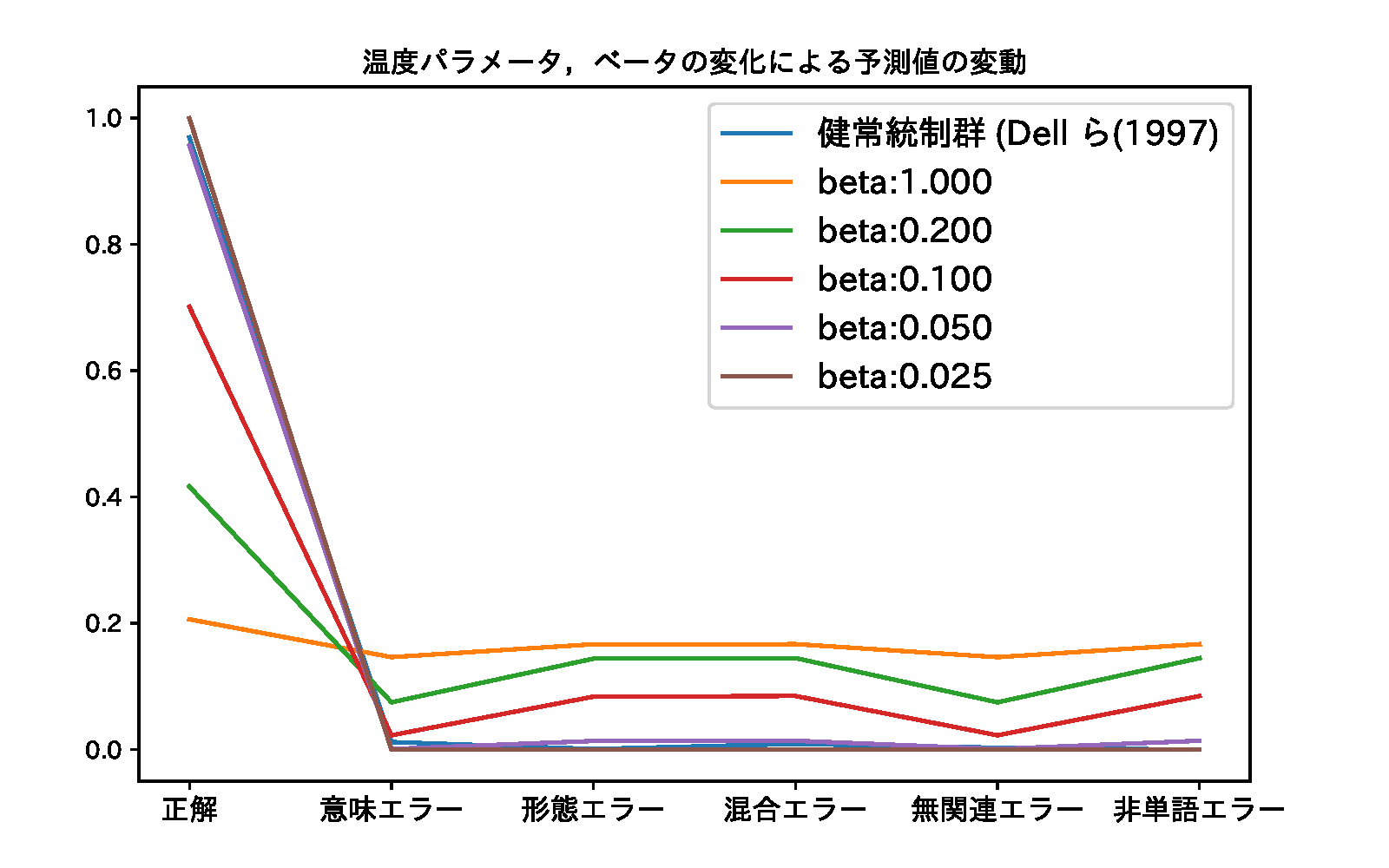
図 ソフトマックス関数において，温度パラメータを変化させた場合の各反応カテゴリの確率密度の変化。 ただし図中の
\[ \ell \equiv \sum_i t_i\log p_i + (1-t_i)\log(1-p_i), \]
Dell のパラメータ推定法と本提案手法との相違は，以下のとおりである。 Dell のパラメータの推定方法は，一回の試行で最大出力を示す音韻層ユニットのカテゴリを反応とみなし，これを 175 回繰り返す。 得られたデータを集計して，各反応カテゴリーの確率を求める。求めた反応確率の値が，患者から得られたデータと異なる場合には，パラメータを修正して， シミュレーションを繰り返す。これを，実際の患者のデータと合致する反応確率が偉えるまで繰り返す，というものである。 GPU を使って 6 次元の確率分布を得るために，予め数千のデータ点を事前に計算し，事前に計算した点に合致するパラメータの値を出力する，であった。 従って，一組のパラメータを得るためにシミュレーションを 175 回繰り返し，さらに，探索空間を徘徊するため，膨大な計算時間を要した。
一方，本提案手法では，機械学習やニューラルネットワークで一般に用いられている勾配降下法を使って，得られたデータに合致するパラメータを探索する。 このため，パラメータの探索は一度で済む。
教師信号 \(\mathbf{t}=[0.97, 0.01, 0.00, 0.01, 0.00, 0.00]\) とする。 このとき最小化すべき目的関数(損失関数，誤差関数) \(l\) を次のように定義する:
\[ l\left(p,x;\theta\right)\equiv\sum_i\left( t_i\log(p_i) + (1-t_i)\log(1-p_i)\right)\tag{1} \]
\[ \frac{\partial l}{\partial p}=\sum_i\left( \frac{t_i}{p_i}-\frac{1-t_i}{1-p_i} \right) = \sum_i\frac{t_i(1-p_i)-p_i(1-t_i)}{p_i(1-p_i)} = \sum_i\frac{t_i-p_i}{p_i(1-p_i)} \]
この \(l\) を最小化する学習をニューラルネットワークの学習則に従い以下のような勾配降下法を用いて訓練する: \[ \Delta\theta = \eta\frac{\partial l}{\partial\theta} = \eta\frac{\partial l}{\partial p}\frac{\partial p}{\partial x_t}\frac{\partial x_t}{\partial\theta} \]
合成関数の微分則に従って \(\displaystyle\frac{\partial l}{\partial\theta}=\frac{\partial l}{\partial p}\frac{\partial p}{\partial x}\frac{\partial x}{\partial\theta}\) である。
更に \(p_i\) を \(x_{j,t}\) で微分，すなわちソフトマックスの微分: \[ \begin{aligned} \frac{\partial p_i}{\partial\beta x_i} &=\frac{e^{\beta x_i}\left(\sum e^{\beta x_j}\right)-e^{\beta x_i}e^{\beta x_i}}{\left(\sum e^{\beta x_j}\right)^2}\\ &=\left(\frac{e^{\beta x_i}}{\sum e^{\beta x_j}}\right) \left(\frac{{\sum e^{\beta x_j}}-e^{\beta x_j}}{{\sum e^{\beta x_j}}}\right)\\ &=p_i \left(\frac{\sum e^{\beta x_j}}{\sum e^{\beta x_i}} -\frac{e^{\beta x_i}}{\sum e^{\beta x_j}}\right)\\ &=p_i (1-p_j) \end{aligned} \]
\[ \frac{\partial p_i}{\partial x_j} = p_i(\delta_{ij}- p_j) \]
\(\theta\) を \(\beta\) とそれ以外 (\(w,d,s,p\)) とに分けて考える。
更に，各個のパラメータについて微分することを考える。 Dell らのモデルでは次式のような漸化式が用いられた: \[ x_{t+1} = (1-d)x_{t} + \sum w x_{t} + z, \]
ここで \(z\sim\mathcal{N}\left(0,a_1^2 + a_2^2x_{t}\right)\) である。
\[ \Delta \theta=\eta\frac{\partial l}{\partial\theta} \]
ここで \(l\) は損失関数 (誤差関数，目的関数) であり，\(\eta\) は学習係数 learning ratio である。
\[ \begin{aligned} \frac{\partial l}{\partial\theta} &=\frac{\partial l}{\partial p}\frac{\partial p}{\partial x_t}\frac{\partial x_t}{\partial\theta}\\ &=\sum_i\frac{t_i-p_i}{p_i(1-p_i)}\sum_j p_i\left(\delta_{ij}-p_j\right)\frac{\partial x_{j,t}}{\partial\theta}\\ \end{aligned} \]
今一度，損失関数を \(l\), 最終層出力の出力を確率密度関数を \(y\), 各ニューロンの出力値を \(x\) とする。 推定すべき Dell モデルのパラメータ \(\theta=\{w,d,s,p\}\) とする。それぞれ
\(x_{i,\tau}^{(\text{Layer})}\) を \(\text{Layer}=\left[s:\text{視覚的意味層}, l:\text{語彙層}, p:\text{音韻層}\right]\) を時刻 \(\tau\) での層(Layer) における \(i\) 番目のニューロンであるとすれば，次式を得る:
\[ \begin{array}{ll} x_{i,t+1}^{(s)} &= (1-d)x_{i,t}^{(s)} + sw \sum_j u_{ij}^{(l)}x_j,\\ x_{i,t+1}^{(l)} &= (1-d)x_{i,t}^{(l)} + sw \sum_{j\in(s)} u_{ij}^{(s)}x_j^{(s)} + pw\sum_{j\in(p)}u_{ij}^{(p)}x_j^{(p)},\\ x_{i,t+1}^{(p)} &= (1-d)x_{i,t}^{(p)} + pw \sum_{j\in(l)} u_{ij}^{(l)}x_j^{(l)},\\ \end{array} \]
\[ \mathbf{\Theta}= \left( \begin{array}{ccc} 1-d & wp & 0\\ wp & 1-d & ws\\ 0 & ws & 1-d\\ \end{array} \right) \] とすれば，
\[ \mathbf{x}_t=\mathbf{\Theta x}_{t-1}+ z\left(\mathbf{x}_{t-1};a_1^,a_2^2\right) \]
%\(\sum_k u_k x_{k,t-1}\) を 1 時刻前の各層のニューロンを \(x_{i,t-1}\) として， \(\theta=\{w,d,s,p\}\)
\[ \frac{x_{j,t}}{\partial d} = -x_{j,t-1}, \hspace{1em} \frac{x_{j,t}}{\partial w} = \frac{x_{j,t}}{\partial s} = \frac{x_{j,t}}{\partial p} = x_{j,t-1} \]
Foygell & Dell (2000) の 表2 に記載されている患者の成績をすべて実施した結果を以下に示した。
ところで，上記シミュレーションで参考にした Foygell & Dell (2000) Tab. 2 だが， 6 つの各反応カテゴリを合算しても 1.0 にならない。 加えて，小数点以下 4 桁まで表示している意味は不明である。 なぜなら，各患者のデータは PNT 検査の結果であるから，175 枚の図版に対する応答である。 すなわち，各カテゴリの正答率は倍精度浮動小数点で次のようになる。 1/175 = 0.005714285714285714 各患者の正答率は，この値の整数倍である。 実際に，小数点第 4 位で四捨五入すると，
164 正解で 0.9371, 165 正解だと 0.9429 となり，W.B. の correct 反応 0.9400 になることはない。 このことから，Dell らのグループでは，演算精度に関して無頓着ではないかと推察される。
Dell モデルの簡便解法デモimport numpy as np
i=0; p=0; u = 1/175; constant = 160
for i in range(10):
n = i + constant
print(f'正解数:{n} その確率:{np.round(u * n, decimals=4):.04f}')
これについては，相互活性化モデルの性質上，ある層の変化を別の層の変化が補うことが起こりうる。 逆に考えれば，リハビリテーションの進行，回復モデルとしては，任意の分野の損傷を他の分野が補完するような機序が想定できるのかも知れない。
このような視点から，回復モデルについて新たに検討できる可能性があるかも知れない。
また，前口上で示したような Rapp のモデル分類学についての検討も含めて考える必要があるだろう。
提案手法は，
本提案手法は，従来手法よりも簡便で，かつ，より妥当性の高い線画命名課題シミュレーションを可能にした。 また，提案手法ではソフトマックス関数に温度パラメータを導入することで，線画命名反応の確率的変動をシミュレートすることを目指した。
温度パラメータが低ければ決定論的，安定的になり，反応が高ければ，反応は不安定になることを表現可能である。 前者は健常者の反応と見なしうるのに対して，後者は反応が検査時毎に安定しないような患者の課題成績と見なしうるだろう。
このことにより，健常モデルと障害者のモデルとを継ぎ目なく，かつ，単一パラメータで表現可能となる。
Roelofs (2019) 失語症における単語検索の音韻キューイング: 即時効果と治療効果のシミュレーションからの洞察 Phonological cueing of word finding in aphasia: insights from simulations of immediate and treatment effects, オリジナルソースコード Roelofs, A., Piai, V., Garrido Rodriguez, G., & Chwilla, D. J. (2016) 絵画命名課題における言語間の干渉と促進の電気生理学的研究 Electrophysiology of cross-language interference and facilitation in picture naming, オリジナルソースコード Roelofs, (2018) 絵画命名時の累積意味効果， 意味遮断効果， 意味撹乱効果の統一的な計算論的説明 A unified computational account of cumulative semantic, semantic blocking, and semantic distractor effects in picture naming オリジナルソースコード， 論文中にはソースコードのアドレスとして https://osf.io/b2mvu/ が記載されているが，アップデートされている。 新 URLは https://osf.io/6ysp2/Ackley, D. H., Geoffrey E. Hinton, and Terry J. Sejnowski. 1985. “A Learning Algorithm for Boltzmann Machines.” Cognitive Science 9: 147–69.
Chen, Ting, Simon Kornblith, Mohammad Norouzi, and Geoffrey Hinton. 2020. “A Simple Framework for Contrastive Learning of Visual Representations.” ArXiv Preprint [cs.LG] (arXiv:2002.05709).
Dell, Gary S. 1986. “A Spreading-Activation Theory of Retrieval in Sentence Production.” Psychological Review 93 (3): 283–321.
———. 1988. “The Retrieval of Phonological Forms in Production: Tests of Predictions from a Connectionist Model.” Journal of Memory and Language 27: 124–42.
Dell, Gary S., Elisa N. Lawler, Harlan D. Harris, and Jean K. Gordon. 2004. “Models of Errors of Omission in Aphasic Naming.” Cognitive Neuropsychology 21: 125–45. https://doi.org/http://dx.doi.org/10.1080/02643290342000320.
Dell, Gary S., Myrna F. Schwartz, Nadine Martin, Eleanor M. Saffran, and Deborah A. Gagnon. 1997. “Lexical Access in Aphasic and Nonaphasic Speakers.” Psychological Review 104 (4): 801–38.
Hinton, Geoffrey E., and Terry J. Sejnowski. 1986. “Learning and Relearning in Boltzmann Machines.” In Parallel Distributed Processing: Explorations in the Microstructures of Cognition, edited by James L. McClelland and David E. Rumelhart, 1:282–317. Cambridge, MA: MIT Press.
Jaiswal, Ashish, Ashwin Ramesh Babu, Mohammad Zaki Zadeh, Debapriya Banerjee, and Fillia Makedon. 2020. “A Survey on Contrastive Self-Supervised Learning.” ArXiv Preprint [cs.CV] (arXiv:2011.00362).
Levelt, Willem J. M. 1989. Speaking from Intention to Articulation. ACL-MIT Press Series in Natural-Language Processing. MIT Press.
Levelt, Willem J. M., Ardi Roelofs, and Antje S. Meyer. 1999. “A Theory of Lexical Access in Speech Production.” Behavioral and Brain Sciences 22: 1–38.
McClelland, James L. 2013. “Integrating Probabilistic Models of Perception and Interactive Neural Networks: A Historical and Tutorial Review.” Frontiers in Psychology 4 (503). https://doi.org/doi:10.3389/fpsyg.2013.00503.
McClelland, James L., Daniel Mirman, Donald J. Bolger, and Pranav Khaitan. 2014. “Interactive Activation and Mutual Constraint Satisfaction in Perception and Cognition.” Cognitive Science 38: 1139–89. https://doi.org/10.1111/cogs.12146.
McClelland, James L., and David E. Rumelhart. 1981. “An Interactive Activation Model of Context Effects in Letter Perception, I: An Account of Basic Findings.” Psychological Review 88 (5): 375–407.
Morton, John. 1969. “INTERACTION of Information in Word Recognition.” Psychological Review 76 (2): 165–78.
Oord, Aaron van den, Yazhe Li, and Oriol Vinyals. 2018. “Representation Learning with Contrastive Predictive Coding.” ArXiv Preprint [cs.LG] (arXiv:1807.03748).
Roach, April, Myrna F. Schwartz, Nadine Martin, Rita S. Grewal, and Adelyn Brecher. 1996. “The Philadelphia Naming Test: Scoring and Rationale.” Clinical Aphasiology 24: 121–33.
Roelofs, Ardi. 1992. “A Spreading-Activation Theory of Lemma Retrieval in Speaking.” Cognition 42: 107–42.
———. 1997. “The Weaver Model of Word-Form Encoding in Speech Production.” Cognition 64: 249—284.
———. 2005. “Spoken Word Planning, Comprehending, and Self-Monitoring: Evaluation of Weaver++.” In Phonological Encoding and Monitoring in Normal and Pathological Speech, edited by R. J. Hartsuiker, R. Bastiaanse, A. Postma, and F. Wijnen, 42–63. Psychology Press.
———. 2014. “A Dorsal-Pathway Account of Aphasic Language Production: The Weaver++/Arc Model.” Cortex 59: 33–48. https://doi.org/http://dx.doi.org/10.1016/j.cortex.2014.07.001.
———. 2019. “Phonological Cueing of Word Finding in Aphasia: Insights from Simulations of Immediate and Treatment Effects.” Aphasiology. https://doi.org/https://doi.org/10.1080/02687038.2019.1686748.
Selfridge, Oliver G. 1958. “Pandemonium: A Paradigm for Learning.” In Mechanisation of Thought Processes: Proceedings of a Symposium Held at the National Physical Laboratory, 1:513–26. London, HMSO.